The asymmetrical load flow is suitable for calculating three-phase symmetrical systems, where the loads of the three phases are not symmetrically distributed. These asymmetrical loads are the source of imbalance between the three phases. This is noticeable because the three phase currents are not equal to each other and no longer have a 120 degrees phase shift. As a result, the voltages in the network will also be in imbalance.
All network parameters are calculated from the parameters that are used by the symmetrical load flow and asymmetrical short-circuit calculations. The calculation uses the symmetrical components method, as used by the IEC 60909 method. The unbalanced load flow data are derived from the normal system impedance (Z1), the inverse-sequence impedance (Z2) and the zero-sequence impedance (Z0). The inverse-sequence impedance is equal to the normal system impedance, but the zero-sequence is usually modelled based on special measurements.
Since the method is based on transmission system modelling, the neutral system and the star-points are not explicitly modelled. The voltage at the star-point and the neutral system can be derived from the zero-sequence current and impedance of the zero-sequence system. Since there is no unambiguous relation between the neutral system and the zero-sequence impedance in the model, this can only take place outside Vision.
The model and calculation method are based on the TCIM (Three Conductor Injection Method). This method is based on current injections on the phase nodes. The system of equations is solved using a Newton-Raphson solver, with a Jacobian for three phase systems.
Node model
As usual in the transmission-oriented approach, a node is represented by three phase nodes. Neutral nodes are not modelled explicitly.
Load model
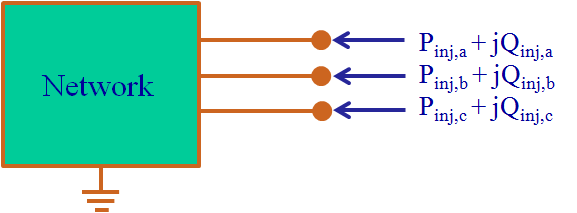
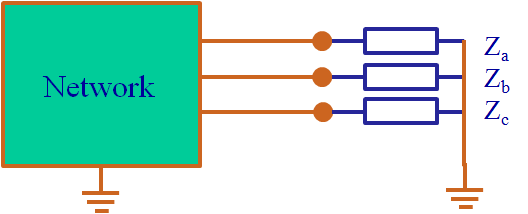
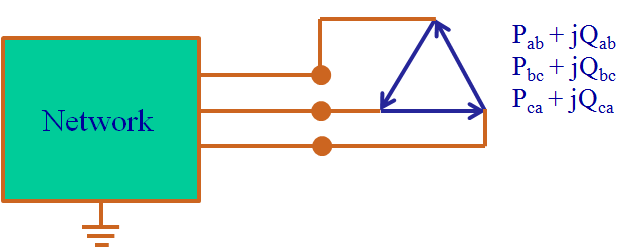
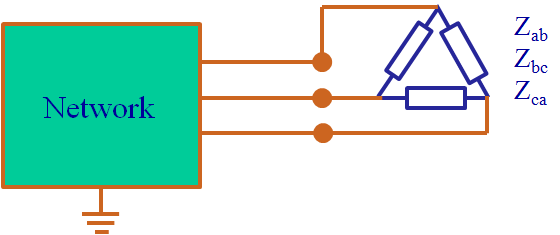
The load can be connected in star (Wye) or delta. In delta connection, no earth connection exists. In star connection, the neutral point may be connected to earth. If an earth connection exists, a return current flows in the zero-sequence system.
The voltage dependency can be defined from percentages of:
•constant power
•constant current
•constant impedance.
Load in star (Wye) connection:
|
|
Constant power |
Constant impedance |
Load in delta connection:
|
|
Constant power |
Constant impedance |
Cable and connection model
Cables and connections (lines) are modelled as balanced components. The inverse-sequence impedances are equal to the normal system impedances (Rac, X, C). The zero-sequence impedances (R0, X0, C0) should be specified by the user.
Reactance coil model
The inverse-sequence impedance Z2 of a reactance coil may be specified by the user. In case no inverse-sequence impedance is known, the same value as the normal system impedance Z1 can be used.
Transformer model
Transformers are assumed to be balanced components. The unbalanced load flow takes into account the windings configuration and the phase shift. The transformer parameters are the same as for the balanced load flow calculation. The zero-sequence impedance needs to be specified.
Voltage regulator
Based on an MV-system voltage regulator (auto transformer), the special transformer "Auto YN0, asymmetric" has been introduced. This transformer can balance the unequal voltages in the distribution system. The voltage regulator of this transformer can change the tap setting for each of the three phases independently of each other. Also, for this transformer, on the "General" tab, the tap change can be manually adjusted for each or the three phases separately.
Network source model
The network source is supposed to be balanced. Its parameters are equal to those for the balanced load flow and for the short-circuit calculations.
See also: