Belasting en opwekking

Hoofdstuk 3 gaat uitgebreid in op de belastingen en de opwekking van het elektrische vermogen. Hierbij wordt aandacht besteed aan het lange, middellange en korte termijngedrag van de belasting. Met name voor de korte termijn wordt het stochastische gedrag van de belasting toegelicht. Verder worden nieuwe ontwikkelingen op het gebied van verbruik en decentrale opwekking toegelicht.

---

3 Belasting en opwekking

3.1 Inleiding

Kennis van de belasting en opwekking is een fundamentele voorwaarde voor het dimensioneren van elektriciteitsdistributienetten. Voor het ontwerpen van een distributienet, dat jaren in de toekomst economisch moet zijn, moet uit gegaan worden van gefundeerde aannames betreffende het gevraagde en het geproduceerde vermogen en de ontwikkeling ervan. De netplanner moet aan de hand van berekeningen aantonen dat het ontwerp zal resulteren in een economisch optimum. Bij deze berekeningen moet de planner kunnen omgaan met enerzijds grote hoeveelheden zich gelijksoortig gedragende belastingen en kleine decentrale opwekeenheden en anderzijds kleine hoeveelheden zich niet gelijksoortig gedragende grote belastingen en opwekeenheden.

Een distributienet wordt ontworpen om tenminste gedurende 40 jaar in de toekomst ongestoord elektrisch vermogen van voldoende kwaliteit te leveren aan de aangeslotenen. De energietransitie zal in de toekomst leiden tot het aansluiten van nieuwe belastingen en opwekkers, zoals grote aantallen gelijksoortige warmtepompen, micro WKK’s, zonnepanelen, een geleidelijk groeiend aantal elektrische auto’s en airconditioning systemen. Het toekomstige distributienet moet zodanig ontworpen worden dat grote aanpassingen vermeden kunnen worden. Hierom is kennis van de ontwikkeling van belasting en opwekking van groot belang.

3.2 Belasting

De belasting is ingedeeld in diverse categorieën. Hierbij wordt een uitspraak gedaan over het gedrag als functie van de tijd en als functie van de netspanning. Het spanningsafhankelijke gedrag komt in het hoofdstuk over de modellering aan de orde. Dit hoofdstuk behandelt voornamelijk het gedrag in de tijd, voor de korte, de middellange en de lange termijnen. De korte termijn betreft het momentane gedrag binnen maximaal ongeveer één uur. De middellange termijn betreft het gedrag over een beperkte periode waarbinnen geen sprake is van groei, zoals één dag of één week. De lange termijn betreft een periode van meerdere jaren, eventueel in combinatie met een periodiek middellang termijngedrag.

Er zijn veel manieren denkbaar om de belastingen in categorieën in te delen. Ieder bedrijf hanteert een eigen methode. Een veel gebruikte methode is (EnergieNed, 1996):

1. Zakelijk kleinverbruik
2. Huishoudelijk kleinverbruik
    a. vrijstaande woningen
    b. eengezinswoningen
    c. etagewoningen
3. Gemengd kleinverbruik (zakelijk en huishoudelijk)

Het is onvermijdelijk dat met name in de categorie ‘zakelijk kleinverbruik’ de diversiteit vrij groot kan zijn. Belastingen in de categorie ‘huishoudelijk kleinverbruik’ zullen een veel uniformer karakter vertonen. Over de categorie ‘gemengd kleinverbruik’ is op voorhand niets te zeggen, omdat deze afhangt zowel van de soort van zakelijk verbruik als van de verdeling tussen zakelijk en huishoudelijk verbruik. Een nadere definitie van deze categorieën zal door de netontwerper zelf gemaakt moeten worden. Een en ander hangt uiteraard af van de nauwkeurigheid die men verwacht te halen.

Belastingen in de categorieën zakelijk of huishoudelijk verbruik vertonen door het hele jaar heen een gelijksoortig gedrag. Specifieke belastingen, zoals warmtepompen en elektrische auto’s stellen hoge eisen aan het distributienet en vragen om een speciale benadering. Belastingen in de categorie ‘warmtepompen’ zullen met name in de koude periode veel elektriciteit verbruiken. Belastingen in de categorie ‘elektrische auto’s’ zullen met name na de ochtend- en avondspits veel elektriciteit verbruiken.

Op deze plaats moet vermeld worden dat decentrale opwekking speciale aandacht verdient. Op locaties waar op grote schaal micro-warmte/kracht of zonnepanelen worden toegepast speelt decentrale opwekking een grote rol in de beschouwingen over de stroombelasting van het distributienet. Afhankelijk van de concentraties kan de belastingstroom in het distributienet worden gecompenseerd of zelfs van richting veranderen. Een aansluiting kan zowel vermogen ontvangen als leveren.

3.3 Lange termijngedrag van de belasting

De belastingen in een distributienet vertonen een jaarlijkse groei (accres). Het accres wordt meestal in procenten ten opzichte van de uitgangsdatum aangegeven. Distributienetten worden zodanig gedimensioneerd dat het accres binnen de economische levensduur niet leidt tot grote aanpassingen. Dit betekent dat de netten worden ontworpen voor de maximale belasting die optreedt aan het einde van hun economische levensduur. Voor de prognose moet de netplanner inzicht hebben in:

• belastinggroei door toename van het aantal aansluitingen
• belastinggroei door groei als gevolg van wijzigend gedrag van de klant.

Het aantal aansluitingen wordt voornamelijk bepaald door de planologie van landelijk tot regionaal niveau. Voor de hogere netniveaus, zoals transformatoren en middenspanningsnetten, bestaat het accres voor een belangrijk deel uit belastingtoename als gevolg van groei in het aantal aansluitingen. Er bestaat een eenvoudige benadering, die gebruik maakt van de aantallen aansluitingen en het gemiddelde jaarverbruik van het specifieke type aansluiting.

Naast de toename van het aantal aansluitingen is een prognose van de belastingontwikkeling van bestaande aansluitingen belangrijk. Hierbij moeten schattingen en keuzes gemaakt worden ten aanzien van:

• het toekomstige gedrag van de klant
• technische ontwikkelingen in elektrische apparatuur
• mogelijkheden voor belastingsturing.

Het toekomstige gedrag van de klant is vrijwel niet te voorspellen. Daarom wordt meestal volstaan met het extrapoleren van historische gegevens van categorieën van klanten, eventueel bijgestuurd door eigen inzicht. Hierbij baseert de netplanner zich op planologische informatie en marktanalyse. Er bestaat geen algemeen bruikbaar model of prognosticeringssysteem. De onzekerheden zijn het grootst in laagspanningsnetten. Hierom ontstaat de trend dat de netontwerper zich steeds meer gaat indekken voor toekomstige onzekerheden en zal hij het laagspanningsnet zo zwaar mogelijk gaan ontwerpen: met maximale kabeldoorsneden en een zo groot mogelijke distributietransformator, van bijvoorbeeld 630 kVA. Ook zal hij bij nieuwbouw extra ruimte claimen om in de toekomst, mocht het nodig blijken, extra netruimten te kunnen plaatsen en zo toekomstige kosten zoveel mogelijk te vermijden.

De technische ontwikkelingen in apparatuur richten zich voornamelijk op het vergroten van de efficiëntie die moet leiden tot energiebesparing. Te denken valt aan energiezuinige verlichting. Aan de andere kant wordt nieuwe apparatuur ontwikkeld die weliswaar efficiënt met energie omgaat, maar wel veel meer elektriciteit verbruikt. De opkomst van nieuwe soorten belastingen zoals warmtepompen en elektrische auto’s heeft dan ook een grote impact op de groei. Hoe lager het netniveau, des te groter deze invloed is. Ook decentrale opwekking is een complicerende factor voor de prognose.

De mogelijkheden voor belastingsturing worden weer actueel door de ontwikkelingen op het gebied van ‘intelligente netwerken’. De ontwikkelingen hebben meestal betrekking op het afstemmen van vraag en aanbod van elektrische energie.

Figuur 3.1 toont de ontwikkeling van het elektriciteitsverbruik in Nederland van 1938 tot 2008 (bron: CBS 2010). Opvallend is de trendbreuk, omstreeks het jaar 1973. Hierdoor is over de hele periode bezien de groei ruwweg in twee tijdvakken verdeeld. In het eerste gedeelte, van 1938 tot 1973 is de groei jaarlijks 8%. Van 1973 tot 2008 is de groei 2,4% per jaar. Hierbij is uitgegaan van een exponentiële groei:

[

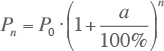
3.1

]

De grafiek toont de door de CBS geregistreerde cijfers en de berekende curve met de hierboven genoemde groeicijfers.

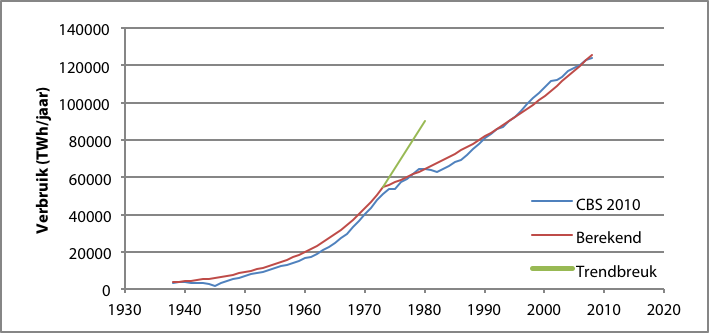
Figuur 3.1 Ontwikkeling van het elektriciteitsverbruik in Nederland tussen 1938 en 2008

Een periode van 70 jaren is meestal te lang voor een redelijke groeiprognose. Er is sprake van een duidelijke trendbreuk omstreeks 1973. Figuur 3.2 toont de ontwikkeling van het elektriciteitsverbruik in Nederland van 1995 tot 2008. Aan de grafiek is een lineaire trendlijn toegevoegd. Over deze periode van 13 jaar is de toename ten opzichte van 1995 bij benadering lineair met 2,4% per jaar.

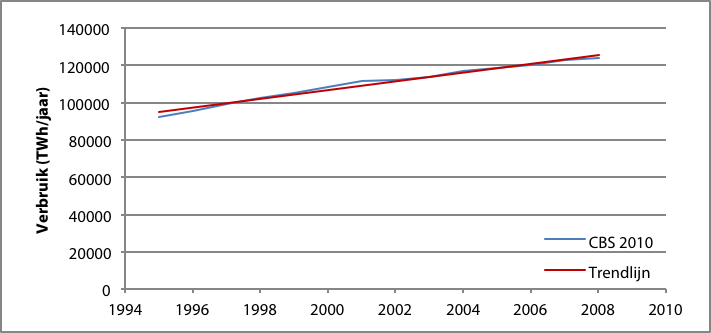
Figuur 3.2 Ontwikkeling van het elektriciteitsverbruik in Nederland tussen 1995 en 2008

Figuur 3.3 toont het verbruik in Nederland in 2008. Het verschil tussen zomer en winter is een kleine 20 procent. Deze grafiek toont aan dat binnen het tijdsbestek van één jaar normaliter geen rekening wordt gehouden met de groei. Wel houdt men rekening met het seizoensafhankelijke gedrag.

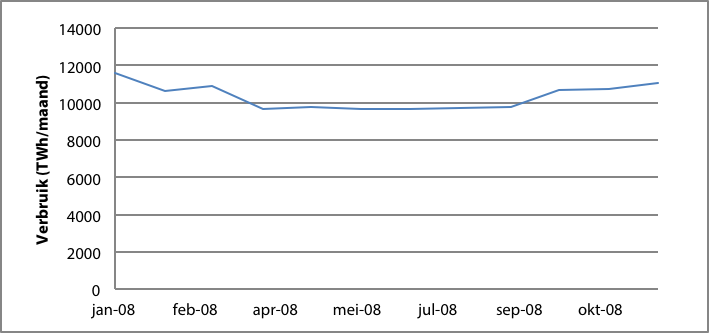
Figuur 3.3 Ontwikkeling van het elektriciteitsverbruik per maand in Nederland in 2008

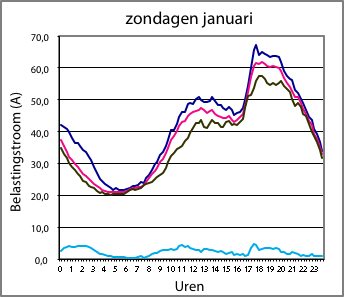
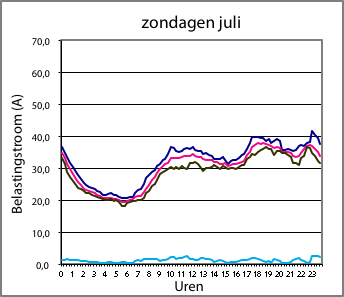
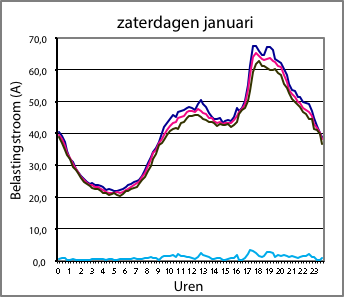
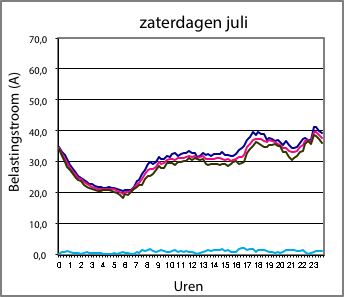
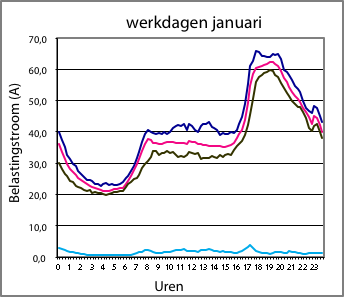
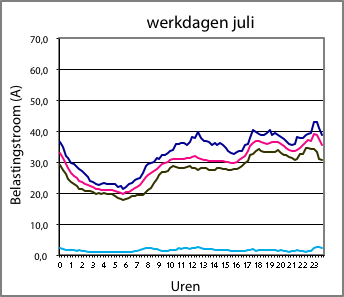
Figuur 3.4 Dagbelastingspatronen in een woonwijk in de winter (links) en in de zomer (rechts). Donkerblauw is maximum, rose is gemiddeld, zwart is minimum; de lichtblauwe lijn is de standaarddeviatie

3.4 Middellange termijngedrag van de belasting

De middellange termijn is een rekbaar begrip. De belasting kan in zekere zin bekend worden verondersteld in deze periode dat de groei en het willekeurige gedrag een minder grote rol spelen. Het gedrag van de belasting wordt dan deterministisch genoemd. Het middellange termijn gedrag beschrijft de belasting over een dag, een week, een maand of een gedeelte van een jaar. Naar gelang de toepassing gebruikt de netplanner de maximum en minimum waarden van de belasting of gebruikt hij belastingspatronen.

De afbeeldingen links geven een voorbeeld van de belastingstromen in een woonwijk, gedurende de winter (links) en de zomer (rechts). Deze woonwijk heeft alleen ‘traditionele’ belastingen. Dat wil zeggen: gewone huishoudelijke apparatuur en verlichting en geen elektrische auto’s, warmtepompen, micro-WKK’s en zonnepanelen. De belastingen op zondag, op zaterdag en op werkdagen lijken sterk op elkaar, zowel in de winter als in de zomer. Voor alle dagen van de week bedraagt het maximum in de zomer ongeveer 60% van het wintermaximum. Het minimum in de zomer is ongeveer gelijk aan het winterminimum. In de vorm van de dagbelastingskromme in de winter is duidelijk het gedrag in de avonduren zichtbaar. Globaal tussen 17:00 en 22:00 uur is de belasting beduidend hoger dan overdag.

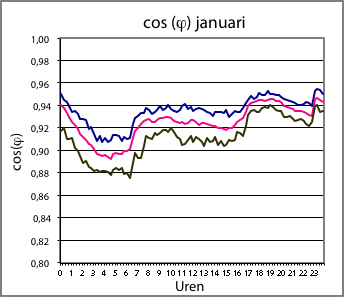
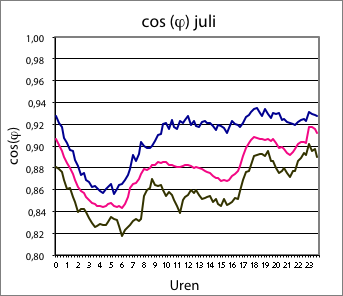
Figuur 3.5 Dagpatronen van de cos(φ) van de belasting in een woonwijk in de winter (links) en in de zomer (rechts)

Figuur 3.5 illustreert het gedrag van de cos(φ) over de werkdagen in januari (links) en juli (rechts). Het valt op dat de cos(φ) in de winter gemiddeld 0,92 bedraagt en in de zomer 0,88. Tijdens de perioden van lage belasting vertoont de cos(φ) lagere waarden dan in perioden van hoge belasting.

De belastingspatronen kunnen worden toegepast op een korte tijdspanne, zoals een dag, maar ook voor een langere tijdspanne, zoals een maand of een jaar. Figuur 3.6 toont het gedrag van de voedingsstroom vanuit het voedingsstation van een 20 kV-streng in een kassengebied gedurende drie weken in september. Een negatieve waarde van de stroom betekent een omgekeerde energierichting. Duidelijk is te zien dat de stroom dagelijks van teken wisselt. Dit betekent dat de som van de stroom van alle aangeslotenen dagelijks wisselt tussen afname en productie. In dit geval komt een belastingstroom van 100 A overeen met een driefasig vermogen van ongeveer 3,5 MVA.

Meting van de belastingen op de individuele knooppunten toont aan hoe de totale voedingsstroom van de streng opgebouwd is uit de som van alle belastingen en generatoren. De grafieken van de generatorvermogens laten zien hoe het aan- en uitschakelen van decentrale opwekking leidt tot dagelijkse schommelingen tot ruim 5 MW per generator.

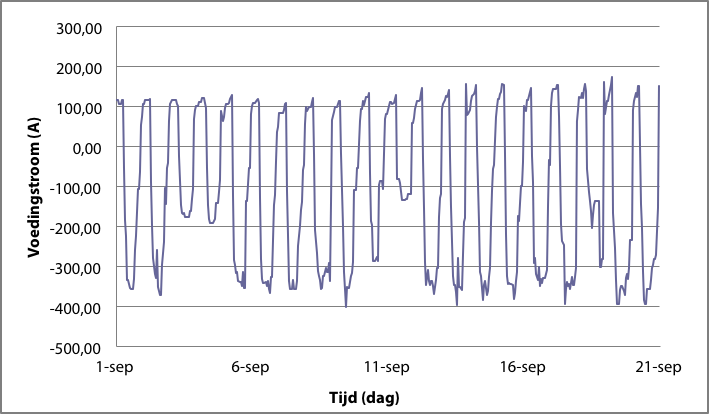
Figuur 3.6 Belastingspatroon van een 20 kV-streng in een kassengebied

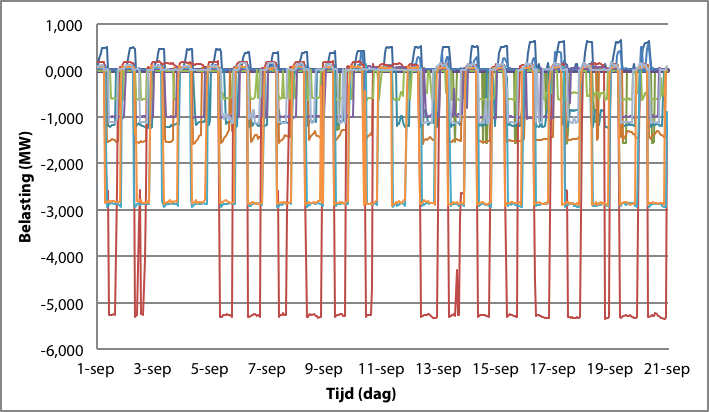
Figuur 3.7 Vermogenspatroon van individuele aansluitingen in een 20 kV-streng in een kassengebied

3.5 Korte termijngedrag van de belasting

Met het gedrag van de belasting in de korte termijn wordt geprobeerd een uitspraak te doen over de belasting ten tijde van het minimum, het maximum of een ander specifiek tijdstip. De belasting bestaat namelijk uit een gedeelte dat vrij goed voorspelbaar is (de middellange termijn) en een gedeelte dat de belasting zich willekeurig gedraagt. Het is voor een woonwijk redelijk goed bekend wanneer het minimum en het maximum van de belasting zich voordoet en hoe groot de waarde daarvan naar verwachting is. Daarbovenop is altijd een zekere willekeurige component die ervoor zorgt dat de maxima van alle individuele belastingen nooit tegelijkertijd optreden en waardoor het maximum van de som van alle belastingen nooit gelijk is aan de som van alle maxima.

In de volgende paragrafen worden de begrippen ‘stochastisch gedrag’ en ‘gelijktijdigheid’ van de belasting nader toegelicht. In bestaande netten zonder elektrische auto’s, warmtepompen, micro-WKK’s en zonnepanelen wordt met de beschreven techniek rekening gehouden met de ongelijktijdigheid van de belastingen. In netten met elektrische auto’s, warmtepompen, micro-WKK’s en zonnepanelen kan echter niet alleen met de zich ongelijktijdig gedragende belasting worden gerekend en moet naast het stochastische gedrag ook rekening gehouden worden met een aanzienlijke component van de belasting die zich met een grote gelijktijdigheid gedraagt. Zo zullen elektrische auto’s worden opgeladen bij thuiskomst aan het einde van een werkdag en zullen warmtepompen met eventueel bijverwarming op koude dagen allemaal gelijktijdig in bedrijf zijn. Als gevolg hiervan zal bij nieuwbouw van netten steeds vaker ontworpen worden op basis van de som van de individuele maximale belastingen, waarbij maar in beperkte mate rekening gehouden wordt met het stochastische gedrag.

3.5.1 Het stochastische gedrag van de belasting

Individuele klanten vertonen in het elektriciteitsverbruik over een etmaal beschouwd een zeker groepsgedrag, maar gedragen zich momen­taan gezien als onafhankelijke individuen. Immers, niet bij iedereen draait de wasmachine op hetzelfde moment. Maar toch vertonen de individuele gebruikers als functie van de tijd, verspreid over een etmaal, gemiddeld genomen grote overeenkomsten in het gedrag. Figuur 3.8, waarin de belastingscurven genormeerd zijn naar hun eigen gemiddelde, illustreert dit. Tussen 1:00 en 7:00 uur is de belasting minimaal. Tussen 7:00 en 9:00 uur neemt de belasting snel toe. ’s Avonds neemt de belasting nog meer toe, om daarna weer af te dalen tot het minimum.

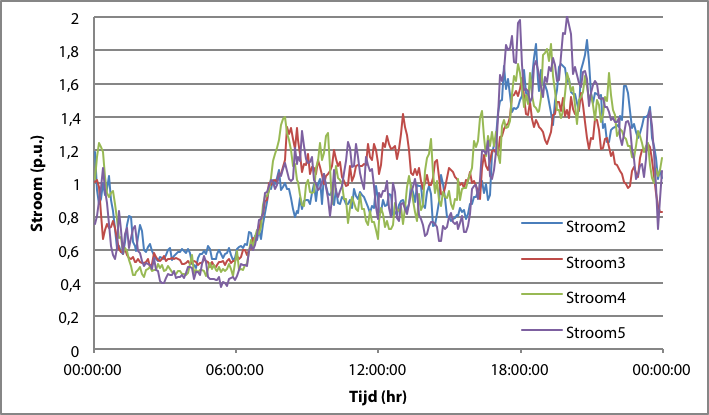
Figuur 3.8 Genormeerde stroomverdeling voor vier afnemers, verspreid over een dag

Het gedrag van de belastingen wordt beschreven door het deterministische gedrag als functie van de tijd en de momentane stochastische parameters, die onafhankelijk zijn. Het deterministische gedrag wordt beschreven met een patroon als functie van de tijd. Een voor de hand liggend patroon is een 24 uurs dagbelastingcurve. De belastingcurven voor groepen belastingen zijn door meetprojecten inmiddels redelijk bekend.

Alle belastingen gedragen zich over de gehele dag genomen als onderling afhankelijke stochastische signalen, maar binnen een beperkt tijdvenster (van bijvoorbeeld één uur) gedragen zij zich als onafhankelijke stochastische signalen. Van die onafhankelijke stochastische signalen kan per tijdvenster een gemiddelde waarde en een spreiding (standaarddeviatie) worden uitgerekend. Figuur 3.9 illustreert dit. Van alle genormeerde belastingskrommen zijn eerst op uurgemiddelden gebaseerde belastings­krommen berekend. Vervolgens zijn deze uurcurven als functie van de tijd uitgezet. Voor elke uurwaarde is de spreiding uitgerekend tussen alle vier de curven. Deze spreiding is als functie van de tijd uitgezet.

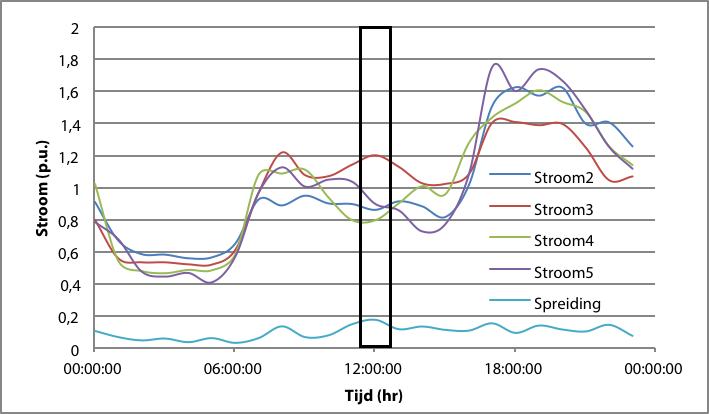
Figuur 3.9 Uurgemiddelden van de genormeerde stroom voor vier afnemers en spreiding

In figuur 3.9 is op t=12 hr een tijdvenster aangegeven. Binnen dat tijdvenster gedraagt de momentane belasting zich als een onafhankelijk stochastisch signaal. De belasting laat zich in ieder tijdvenster beschrijven als een stochastische variabele, met een gemiddelde waarde en een spreiding. Voor het aangegeven tijdvenster in figuur 3.9 is de gemiddelde waarde van de stroom ongeveer gelijk aan 1 pu en de spreiding ongeveer gelijk aan 0,2 pu.

De Centrale Limietstelling stelt dat de kansverdeling van de som van een voldoend groot aantal onafhankelijke stochastische variabelen bij benadering normaal verdeeld is. Dat betekent voor dit geval dat de som van een voldoende aantal onafhankelijke stochastische belastingsignalen zich bij benadering als een normale verdeling gedraagt. Dit wordt bevestigd door Engels (RWTH, 2000) en Livik (CIRED, 1993).

Met deze aanname kan de belasting op een bepaald tijdstip t beschreven worden door een normale kansverdeling met gemiddelde μ(t) en spreiding σ(t). Figuur 3.10 geeft de kansverdeling weer voor een belasting met gemiddelde waarde 3 kW en een spreiding van 1 kW.

Het model van de belasting wordt gecom­pleteerd door de gemiddelde waarden en de spreidingen weer te geven als functies van de tijd. Hiermee is het gedrag van de belasting voor iedere gewenste periode beschreven door een profiel van stochastisch normale verdelingen, gekenmerkt door de tijdfuncties voor de gemiddelden μ(t) en voor de spreidingen σ(t).

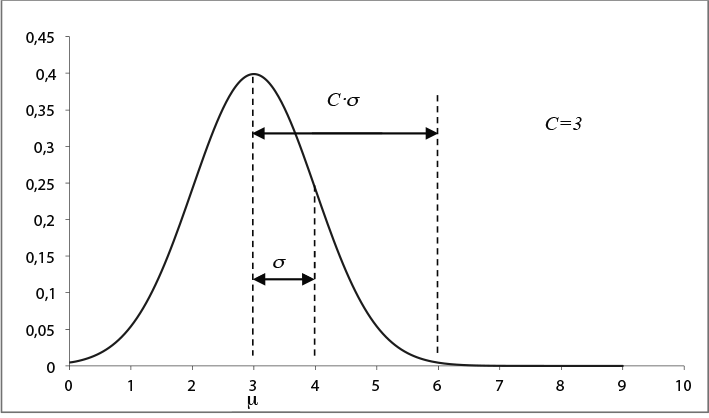
Figuur 3.10 Belasting als normale kansverdeling

Deze modellering gaat op voor gelijksoortige belastingen. Andere typen belastingen moeten separaat gemodelleerd worden, met ieder hun eigen tijdfuncties. Bij gemengde belastingen moet gewerkt worden met combinaties van de separate tijdfuncties. Bijzondere belastingen, zoals zware industrie, landbouwbedrijven en elektrische tractie, alsmede decentrale opwekkers blijven bijzondere aandacht vragen en kunnen niet met deze methode gemodelleerd worden.

In figuur 3.11 is de gemiddelde belastingscurve voor eerder genoemde vier belastingen afgebeeld. Deze kromme is gelabeld ‘mu’. Ook is er met behulp van de spreidingscurve een band aangegeven, waarbinnen zich met een zekere waarschijnlijkheid de individuele belastingscurven zullen bevinden. De boven- en ondergrenzen zijn berekend door de spreidingscurve bij de gemiddelde curve op te tellen (gelabeld ‘mu+s’), respectievelijk af te trekken (gelabeld ‘mu-s’). Indien de stochastische belasting zich op alle tijdstippen als een normaal verdeelde stochastische variabele zou gedragen, zou de werkelijke waarde van de belasting zich met een waarschijnlijkheid van 70% binnen de aangegeven grenzen bevinden.

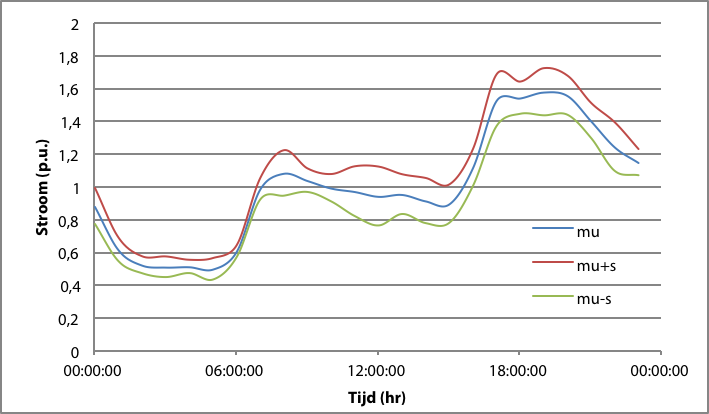
Figuur 3.11 Gemiddelde stroom en 1s grens, over een dag

Alle op deze manier in een streng gemodelleerde belastingen kunnen worden gesommeerd volgens de theorie van de stochastische signalen. Dat heeft gevolgen voor het gemiddelde en de spreiding.

Figuur 3.12 geeft aan hoe dit uitwerkt in een distributienet. Elk grafiekje geeft de kansverdeling weer van de belastingstroom voor respectievelijk het begin, het midden en het einde van een streng. De gemiddelde waarden zijn respectievelijk 50, 20 en 5. De spreiding neemt toe naar het einde van de streng.

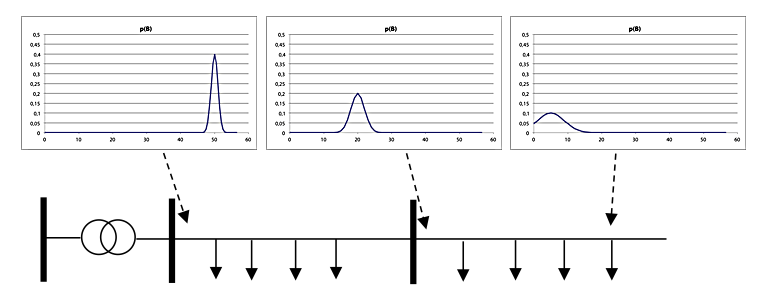
Figuur 3.12 Kansverdelingen van de afnemende stroom in een richting van een distributienet

Dicht bij de voeding is het aantal belastingen, en dus het aantal onafhankelijke stochastische signalen, groot. Doordat de som van het aantal onafhankelijke belastingen verder in het net afneemt, neemt de onzekerheid (en dus de spreiding) toe. Dit komt omdat de maximale belasting bij de verschillende verbruikers op verschillende tijdstippen op zal treden. Dit verschijnsel is eerder beschreven door Rusck. We zien dus dat de gemiddelde waarde afneemt en dat de spreiding in verhouding toeneemt. Een onderzoek heeft aangetoond dat voor afgaande richtingen in het LS-net de aantallen aangeslotenen te klein zijn om de normale verdeling te mogen toepassen. Opvallend resultaat van dit onderzoek was dat rond momenten van de piekbelasting 20% van de aangeslotenen verantwoordelijk was voor 50% van die piek (Provoost, 2011). Voor een klein aantal verbruikers is het dus eigenlijk niet meer correct om de normale verdeling toe te passen.

3.5.2 Gelijktijdigheid van de belasting en het model van Rusck

Voor elk specifiek moment van de dag kan de grootte van de belasting van een specifieke categorie bij benadering voorspeld worden. Het deterministische deel wordt beschreven met behulp van patronen voor bijvoorbeeld een dag. Zo kunnen de momenten geschat worden waarop de belasting minimaal of juist maximaal is. Dit zijn belangrijke waarden voor het dimensioneren van een distributienet. Een distributienet wordt echter niet gedimensioneerd voor de som van de afzonderlijke maximale belastingwaarden van alle aansluitingen, want de maximale belasting van de afzonderlijke aansluitingen zal op verschillende tijdstippen optreden. Dit verschijnsel wordt diversiteit of ongelijktijdigheid genoemd.

Ontwerpberekeningen voor LS- en MS-netten worden doorgaans uitgevoerd door gebruik te maken van maximale belastingen in combinatie met kengetallen voor de gelijktijdigheid ervan. De techniek is gebaseerd op de informatie die de distributiebedrijven jaarlijks vergaarden met verbruiks- en maximaalmetingen op diverse plaatsen in het net.

De maximale belasting P_max is gedefinieerd als de grootste waarde van de belasting voor aansluitingen, kabels of transformatoren. Een index geeft aan op hoeveel aansluitingen de maximale belasting betrekking heeft. De waarde wordt uitgedrukt in kW.

Diversiteit (of ongelijktijdigheid) is het verschijnsel dat de maximale belasting op een punt in het distributienet kleiner is dan de som van de afzonderlijke maximale belastingen van de aansluitingen of van de punten die vanuit het beschouwde punt worden gevoed. De diversiteit treedt op zowel voor alle aansluitingen die op een streng of op een voedingsstation zijn aangesloten als voor alle strengen die op een voedingsstation zijn aangesloten.

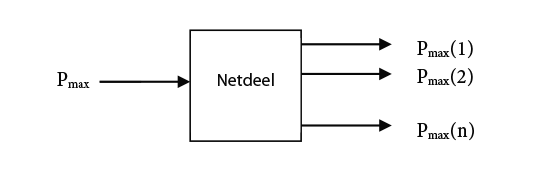
Figuur 3.13 Diversiteit van de belasting

In figuur 3.13 is P_max de voedingsstroom en P_max(i) de maximale belasting in richting i. Voor dit (radiaal bedreven) netwerk geldt:

[

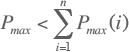
3.2

]

De relatie die de maximale belasting van een deel van het distributienet berekent door gebruik te maken van de gelijktijdigheidsfactor is in 1956 beschreven door Rusck. Het model gaat ervan uit dat de belastingen zich gedragen als stochastisch onafhankelijke variabelen met een normale kansverdeling. Het doel van het model is met behulp van de diversiteit de maximale belasting van componenten, zoals kabels of een voedingstransformator, vast te stellen. De mate van diversiteit wordt beschreven met de gelijktijdigheidsfactor g, die is gedefinieerd als het quotiënt van de maximale belasting P_max,n voor n aansluitingen en de som van de maximale waarden P_max(i) van de afzonderlijke belastingen die vanuit dit punt gevoed worden.

[

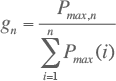
3.3

]

Voor n gelijke belastingen met maximum vermogen P_max,1 gaat vergelijking 3.3 over in:

[

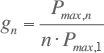
3.4

]

ofwel:

[

3.5

]

Een van de voorwaarden voor het toepassen van het model van Rusck is dat alle belastingen zich gedragen als onderling onafhankelijke normaal verdeelde stochastische variabelen. Echter, over een heel etmaal beschouwd, gedraagt de belasting zich niet als een normaal verdeelde stochastische variabele. Zo kunnen globaal twee tijdvensters worden benoemd voor piek- en dalbelasting. Binnen één tijdvenster kan wel aangenomen worden dat de belasting zich als een normaal verdeelde stochastische variabele gedraagt. Dat specifieke tijdvenster vindt bij voorkeur plaats tijdens de piekbelasting. Volgens de kansrekening kan de stochastische variabele beschreven worden met de gemiddelde waarde in het tijdvenster en een bijbehorende spreiding (standaardafwijking). Het verschil tussen de maximale belasting en de gemiddelde belasting in het tijdvenster is dan evenredig met de spreiding. Voor één aansluiting geldt:

[

3.6

]

waarin:

Pmax,1	maximale belasting van één verbruiker
Pgem,1	gemiddelde belasting van één verbruiker
σ1	spreiding van één verbruiker
C	een constante factor

In een normale verdeling is, theoretisch gezien, het maximum van het argument van de normale verdeling (de belastingswaarde) oneindig. De maximale waarde van de belasting in het distributienet is echter wel degelijk eindig. De factor C legt het verband tussen enerzijds het verschil tussen het maximum en gemiddelde van de belasting en anderzijds de spreiding uit het kansbegrip. Zie figuur 3.10, waar C=3.

Voor een gelijktijdige belasting van n aansluitingen geldt, met dezelfde factor C:

[

3.7

]

Omdat de belasting voor elke gelijksoortige aansluiting zich gedraagt als eenzelfde normale verdeling, geldt voor de spreiding bij n aansluitingen:

[

3.8

]

en voor de gemiddelde belasting van n aansluitingen:

[

3.9

]

Na combinatie volgt uit bovenstaande vergelijkingen:

[

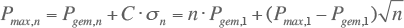
3.10

]

Door vergelijking 3.10 te delen door n·P_max,1 volgt de uitdrukking voor de gelijktijdigheidsfactor:

[

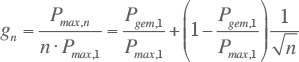
3.11

]

Voor een oneindig aantal aansluitingen geldt:

[

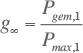
3.12

]

De gelijktijdigheidsfactor voor een oneindig aantal aansluitingen beschrijft het gedrag voor een specifiek belastingstype, onafhankelijk van het aantal aansluitingen. Hiermee gaat de vergelijking voor de gelijktijdigheidsfactor over in de vergelijking van Rusck:

[

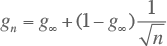3.13

]

Hierdoor kan de formule voor de maximale belasting ook geschreven worden als:

[

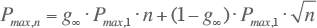
3.14

]

Voor één aansluiting is n=1 en is de gelijktijdigheidsfactor g₁=1. Voor een oneindig aantal aansluitingen geldt n^→∞ en is g_n=g_∞. In praktijk blijkt g_∞ voor de meeste gevallen ongeveer gelijk te zijn aan 0,2. In dat geval is de gelijk­tijdig­heidsfactor g_n voor 80% evenredig met het omgekeerde van de wortel van het aantal verbruikers.

De gelijktijdigheidsfactor hangt sterk af van de homogeniteit van de belasting. Bij een sterk homogene belasting, zoals openbare verlichting, zal de factor ongeveer gelijk aan 1 zijn. Ook de omvang van het beschouwde netgedeelte heeft grote invloed op de waarde.

De locatie van het beschouwde punt is van invloed op de ‘lokale’ diversiteit. In het algemeen zal dichter bij de voeding de lokale gelijktijdigheidsfactor groter zijn dan in een punt dat zich verder weg van de voeding bevindt. Dit komt doordat bij een groot aantal belastingen het willekeurige gedrag wordt ‘uitgemiddeld’. In een verder weg gelegen punt is het aantal aansluitingen kleiner, waardoor het totaal van de belastingen zich grilliger gedraagt. Figuur 3.14 illustreert dit. In knooppunt 1 is de lokale gelijktijdigheidsfactor voor een totaal van n₁ aansluitingen gegeven door g(n₁). Deze waarde is groter dan de lokale gelijktijdigheidsfactor op het verder weg gelegen knooppunt 2 met een totaal van n₂ aansluitingen. Hetzelfde geldt voor knooppunt 3. De totale gelijktijdigheidsfactor in knooppunt 1 voor alle n aansluitingen wordt berekend uit het product van alle achterliggende gelijktijdigheidsfactoren:

[

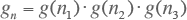
3.15

]

Figuur 3.14 Gelijktijdigheid op diverse locaties in een distributienet

De maximale belasting voor n gelijke aansluitingen wordt berekend uit de gelijktijdigheidsfactor en de maximale belasting voor één aansluiting:

[

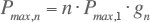
3.16

]

waarbij:

n	het aantal verbruikers
Pmax,1	maximale waarde van de belasting van één aansluiting
gn	gelijktijdigheidsfactor voor n aansluitingen

3.5.3 Relatie tussen elektriciteitsverbruik en de maximale belasting

Het verbruik is de hoeveelheid elektrische energie die per tijdseenheid, meestal per jaar, wordt verbruikt. Het verbruik kan betrekking hebben op één aansluiting, of op een netdeel. Het verbruik V wordt gerepresenteerd in kWh/jaar. Voor de diverse belastingscategorieën is het verbruik per aansluiting in het algemeen beter bekend dan de maximale belasting per aansluiting. Voor het ontwerpen van een distributienet is een relatie nodig tussen verbruik en maximale belasting. Een van de mogelijkheden hiervoor is de bedrijfstijd van de maximale belasting. Deze is gedefinieerd als het quotiënt van het jaarverbruik en de maximale belasting in dat jaar. Hoe groter de diversiteit is, des te kleiner wordt de bedrijfstijd van het maximum.

[

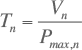
3.17

]

Om een gefundeerde uitspraak te kunnen doen over de maximale belasting van een belastingscategorie, heeft Velander in 1952 vanuit metingen deze relatie met het verbruik proefondervindelijk vastgesteld. Hierbij ging hij ervan uit dat de belastingen zich op een specifiek moment gedragen als onderling onafhankelijke stochastische variabelen. Deze relatie is later in 1975 gebruikt door Strand en Axelsson voor toepassing in een computersysteem dat het verbruik en de maximale belasting van een distributienet administreert.

De relatie van Velander is geschikt voor het berekenen van de maximale belasting van belastingscategorieën. In combinatie met belastingsprognose zijn de modellen van Rusck en Velander de basis voor het ontwerpen van MS en LS-netten.

De formule van Velander luidt (Velander, 1952; Strand-Axelsson, 1975 en EnergieNed, 1996):

[

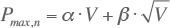3.18

]

waarbij:

Pmax,n	maximale belasting van n aansluitingen (kW)
V	jaarverbruik van n aansluitingen (kWh/jaar)
α, β	door meting vast te stellen parameters

De parameters α, β en V beschrijven de belastingscategorie. Deze parameters zijn afhankelijk van:

• de aard van het gebied
• het type aansluitingen
• het aantal aansluitingen

Door de formule van Velander (3.18) te delen door het aantal aansluitingen volgt de equivalente gelijktijdige maximale belasting per aansluiting op een willekeurige plaats in het beschouwde netdeel, waar n gelijksoortige aansluitingen aanwezig zijn.

[

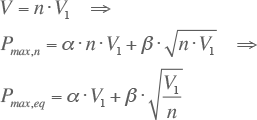
3.19

]

Met de equivalente gelijktijdige maximale belasting per aansluiting wordt als het ware de gelijktijdig maximale belasting van een netdeel verdeeld over alle individuele aansluitingen. De waarde van P_max,eq neemt af bij een toenemend aantal aansluitingen. Het minder grillige gedrag van het belastingspatroon in de buurt van de voedingspunten van een netdeel ten opzichte van de individuele aansluitingen is merkbaar doordat in het tweede gedeelte van de vergelijking gedeeld wordt door √n. Voor een oneindig aantal aansluitingen is de equivalente gelijktijdig maximale belasting per aansluiting gelijk aan α·V₁. Figuur 3.15 illustreert dit. In de grafiek zijn twee curves afgebeeld voor een verbruik van 4300 kWh/jaar en 2300 kWh/jaar. De gebruikte parameters zijn:

α = 0,23·10^-3
β = 0,016

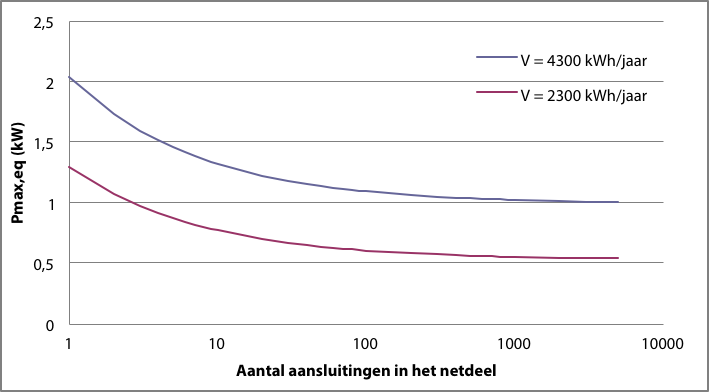
Figuur 3.15 Equivalente gelijktijdig maximale belasting per aansluiting

Door uit te gaan van het specifieke verbruik van één aansluiting kan met de parameters α en β de gelijktijdig maximale belasting voor n aansluitingen worden berekend.

[

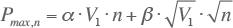
3.20

]

Door vergelijking 3.20 te combineren met de formules van Rusck (3.6 tot en met 3.14) volgen onderstaande relaties.

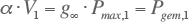
	[	3.21	]
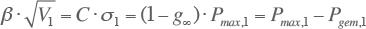
	[	3.22	]

Met deze relaties kunnen de parameters α en β vastgesteld worden indien van de aansluitingscategorie het jaarverbruik en het gemiddelde en maximum vermogen per aansluiting bekend zijn. Hierbij moet worden opgemerkt dat het gemiddelde vermogen P_gem,1 niet gelijk is aan het jaarverbruik gedeeld door het aantal uren in het jaar. Zoals in de vorige paragraaf opgemerkt, gedraagt de belasting zich over een heel etmaal niet als een normaal verdeelde stochastische variabele. Daarom heeft P_gem,1 de gemiddelde waarde van de stochastische variabele die in het beschouwde tijdvenster wel als normaal verdeeld mag worden verondersteld. Dit is de gemiddelde waarde tijdens de piekbelasting.

Indien van een type gebruiker het jaarverbruik voor één aansluiting V₁, de bedrijfstijd T₁ en de gelijktijdigheidfactor voor een oneindig aantal gebruikers g_∞ bekend zijn, kunnen de parameters α en β vastgesteld worden. De maximale belasting voor één aansluiting P_max,1 volgt uit de definitie van de bedrijfstijd en de gemiddelde belasting kan volgens Rusck worden berekend uit de gelijktijdigheidfactor en de gemiddelde belasting:

[

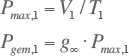
3.23

]

De waarde van g_∞ kan volgens Rusck worden afgeleid uit de gelijktijdigheid van n gebruikers:

[

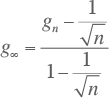
3.24

]

Door deze vergelijkingen in te vullen in de formules die de relaties tussen Velander en Rusck beschrijven, kunnen de parameters α en β vastgesteld worden.

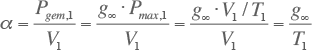
	[	3.25	]
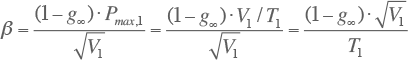
	[	3.26	]

Omgekeerd kunnen de stochastische parameters uit de parameters van Velander worden bepaald. Door de vergelijking van Velander te combineren met de formules van Rusck volgen onderstaande relaties. De gemiddelde waarde van de stochastische belasting volgt uit:

[

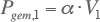
3.27

]

De spreiding van de stochastische belasting wordt hierna berekend met:

[

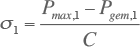
3.28

]

Een aspect als variatie van de belasting kan eenvoudig worden meegenomen in de patronen van de gemiddelden. De spreiding moet wel altijd in de pas blijven met de gemiddelde waarde. Hulpmiddel hiervoor is de constante C. Bij toename van de belasting, zonder dat het aantal aansluitingen toeneemt, moet de spreiding evenredig toenemen.

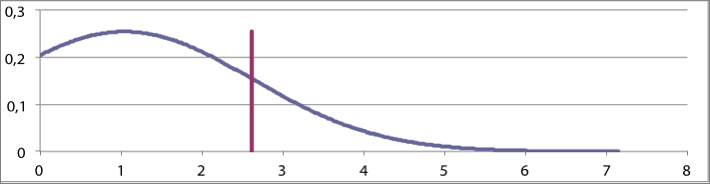
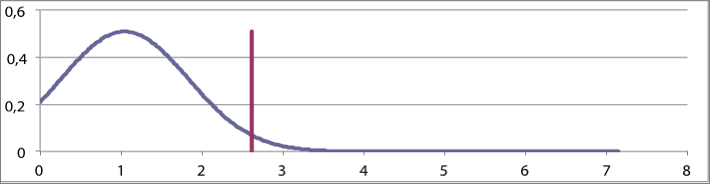
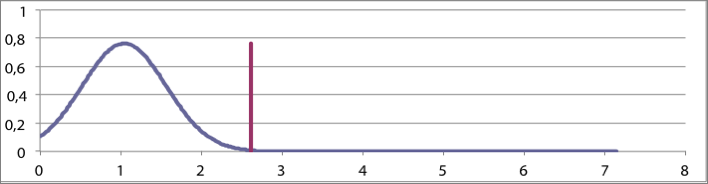
Figuur 3.16 Kansverdelingen voor de belasting als stochastische variabele bij C=1, 2 en 3

De factor C is maatgevend voor de kans dat in het model de stochastische belasting groter is dan de maximale belasting P_max. Met een waarde voor de constante C gelijk aan 1 wordt de maximale waarde van de belasting bepaald door μ+1·σ. Door de eigenschappen van de normale verdeling zal het werkelijke maximum zich met ongeveer 85% zekerheid onder deze μ+1·σ waarde bevinden. Indien de constante C gelijk genomen wordt aan 2, zal het werkelijke maximum zich met ongeveer 97,5% zekerheid onder deze μ+2·σ waarde bevinden. De parameter s1 is afhankelijk van de keuze voor C. Hieronder is de kansverdeling weergegeven voor respectievelijk C = 1, 2 en 3. In figuur 3.16 is in de grafieken met een verticale lijn de waarde van P_max,1 aangegeven. Bij het berekenen van de kansverdelingen is uitgegaan van:

α = 0,23·10^-3
β = 0,023
V₁ = 4500 kWh/jaar
P_gem,1 = α·V₁ = 1,04 kW
P_max,1 = α·V₁ + b·√V₁ = 2,6 kW
g_∞ = P_gem,1/P_max,1 = 0,4
C·σ₁ =P_max,1 – P_gem,1 =1,54 kW
C = 3
σ₁ = 0,51 kW

De grafieken in figuur 3.16 illustreren dat de spreiding omgekeerd evenredig is met de constante C. Zie ook figuur 3.10. Met een kleine waarde van C worden de met deze kansverdeling te berekenen extremen groter. Hiermee moet bij de interpretatie van de resultaten rekening worden gehouden.

Voor het plannen wordt gebruik gemaakt van gemiddelde patronen met een relatief kleine spreiding. Terug­rekenend naar enkelvoudige verbruikers verandert de vorm van het gemiddelde patroon niet, maar wordt de bijbehorende spreiding relatief groter. Deze methode houdt geen rekening met individuele extreme uitschieters. In dat geval zou namelijk de oude methode van rekenen met maximale waarden beter van pas komen.

3.5.4 Vaststellen van de parameters voor korte termijnvariaties met behulp van metingen

De relatie tussen het verbruik en de maximale belasting van een gelijksoortige groep aansluitingen wordt beschreven met de formule van Velander (vergelijking 3.18). Deze formule maakt gebruik van twee parameters α en β, die aan de hand van metingen worden vastgesteld. In het algemeen geldt hierbij dat de metingen voldoende representatief zijn. Aangezien de metingen gezien kunnen worden als een steekproef, geldt volgens de algemene regels van de statistiek dat het aantal metingen (de populatie) groot genoeg moet zijn. Bij het toevoegen van een nieuwe meting aan een verzameling metingen zullen in het algemeen de te bepalen parameters wijzigen. Bij een groter wordend aantal metingen convergeren de parameters naar een vaste ‘werkelijke’ waarde. Hoe groter de populatie, des te beter de parameters de werkelijke waarde benaderen.

Het is van belang de metingen uit te voeren bij een aantal gelijksoortige kenmerken:

• de aard van de gebieden
• het type aansluitingen

Bij het meetprogramma wordt gestreefd naar een zo representatief mogelijke steekproef. Dat betekent dat metingen gedaan zijn aan zowel individuele aansluitingen als aan de LS-kabels en aan de distributietransformator van het voedingsgebied. Daartoe zijn op de aansluitingen, LS-kabels en distributietransformator kWh/kW-meters geplaatst. In een (niet nader gespecificeerde) steekproef bij een netbedrijf zijn metingen verricht aan 18 individuele aansluitingen met jaarverbruiken van 1,5 tot 14 MWh en aan grotere verzorgingsgebieden met jaarverbruiken van 681 tot 10170 MWh.

De parameters van de formule van Velander (vergelijking 3.18) worden gevonden met behulp van de kleinste kwadratenmethode. Deze methode berekent de waarden van de parameters α en β, waarvoor geldt dat de som van de gekwadrateerde verschillen tussen meetwaarden en berekende waarden minimaal is. De methode gaat uit van m meetpunten (x₁, f₁), (x₂, f₂), ... , (x_m, f_m), waarbij x_i een gemeten jaarverbruik is en f_i een gemeten maximum. Deze meetpunten worden benaderd met onderstaande polynoom.

[

3.29

]

De methode van de kleinste kwadraten leidt tot de normaalvergelijkingen van Gauss. Onder de voorwaarde dat, in relatie tot de formule van Velander, de parameter a₀ gelijk is aan nul en dat slechts gezocht wordt naar de parameters a₁ en a₂, leidt dit tot vergelijking 3.30.

[

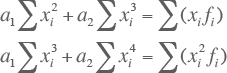
3.30

]

Indien in deze vergelijkingen wordt ingevuld:
a₁ = β
a₂ = α
x₁ = √V_i
f_i = P_i

gaan de normaalvergelijkingen over in:

[

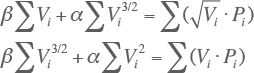
3.31

]

Deze vergelijkingen kunnen ook geschreven worden als:

[

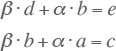
3.32

]

Waarin:

[

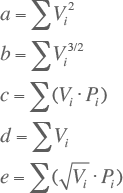
3.33

]

Dit zijn twee vergelijkingen met twee onbekenden α en β die eenvoudig worden opgelost. Na uitwerken van de sommaties voor alle meetwaarden volgt uiteindelijk voor de parameters α en β:

[

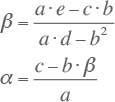3.34

]

Met bovenstaande methode wordt uit de metingen van de steekproef berekend: a = 0,25·10^-3 en b = 0,04. Figuur 3.17 geeft de metingen en de curve in één grafiek weer. De diversiteit van de metingen is groot. De methode schat de parameters op basis van de kleinste som van de afwijkingen in het kwadraat. Dat heeft tot gevolg dat de meetpunten met grote maximum belasting zwaarder wegen dan meetpunten met kleine maximum belasting. Deze methode verdient de voorkeur vanwege de wet van de grote aantallen in de statistiek. Echter, het model moet ook representatief zijn voor de kleine aantallen. Afbeelden van de gegevens in een grafiek met dubbel-logaritmische schaal geeft meer inzicht in de afwijkingen van de metingen ten opzichte van de curve.

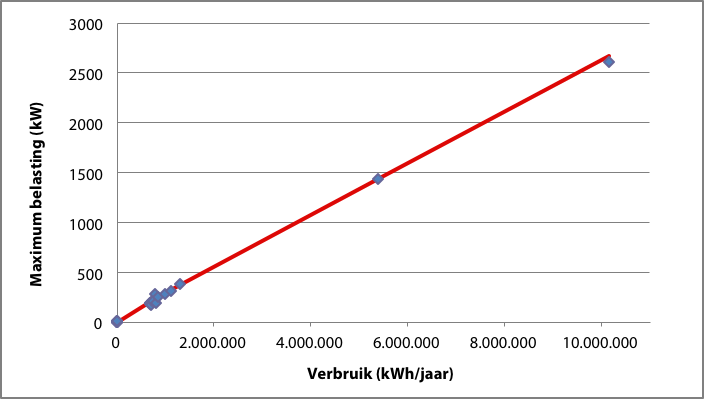
Figuur 3.17 Meetpunten en berekende curve, afgebeeld op lineaire schaalverdeling

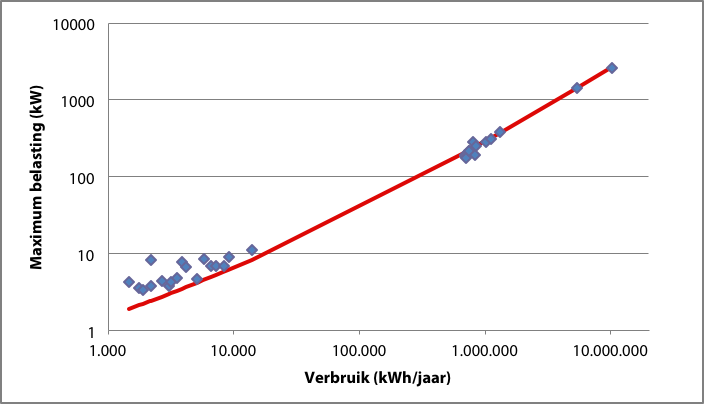
Figuur 3.18 Meetpunten en berekende curve, afgebeeld op dubbel-logaritmische schaalverdeling

De diversiteit in de metingen is goed zichtbaar in de grafiek. Zichtbaar zijn een groep metingen aan kleinverbruikers, een aantal metingen aan kleine distributietransformatoren en twee metingen aan grote distributietransformatoren. Bestudering van de grafieken van figuur 3.17 en figuur 3.18 leert dat de curve een goede representatie is van de metingen aan grotere belastingen. Voor de metingen in de groep van kleinverbruikers is de curve niet representatief.

Indien in de formule van Velander het jaarverbruik van n aansluitingen geschreven wordt als het product van het gemiddelde jaarverbruik van één aansluiting en het aantal aansluitingen, gaat deze over in:

[

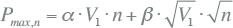3.35

]

Hierin is goed te zien dat de parameter α gelijke invloed heeft voor zowel kleine aantallen als grote aantallen aansluitingen. De parameter β heeft door het wortelteken van n verhoudingsgewijs meer invloed voor kleine aantallen aansluitingen.

De grafieken in figuur 3.19 illustreren de invloed van variatie van de parameter α op de ligging van de curve ten opzichte van de meetpunten. De eerste afbeelding toont de grafiek in lineaire schaal en de tweede afbeelding in dubbel-logaritmische schaal. De afbeeldingen illustreren dat variatie van parameter α een gewone lineaire invloed heeft op de curves. Voor het oplossen van de afwijkingen ten opzichte van metingen van weinig verbruik en lage belasting levert variatie van α geen juiste correctie.

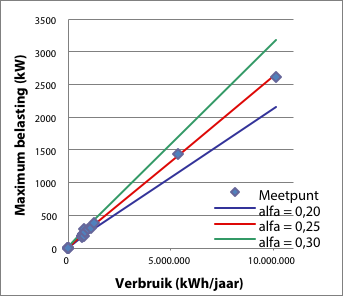
Figuur 3.19 Variatie van parameter α, afgebeeld met lineaire en dubbel-logaritmische schaalverdeling

De grafieken in figuur 3.20 illustreren de invloed van variatie van de parameter β op de ligging van de curve ten opzichte van de meetpunten. De eerste afbeelding toont de grafiek in lineaire schaal en de tweede afbeelding in dubbel-logaritmische schaal. De afbeeldingen illustreren dat variatie van parameter β juist in de lagere vermogens een relatief grote invloed heeft.

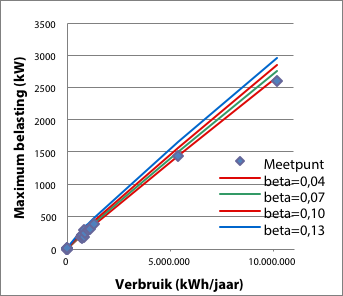
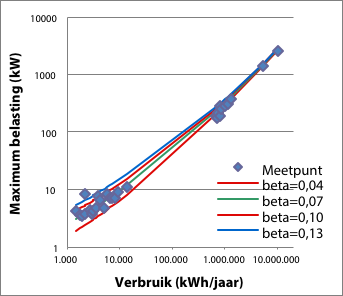
Figuur 3.20 Variatie van parameter β, afgebeeld met lineaire en dubbel-logaritmische schaalverdeling

In de beschreven methode wegen de grote vermogens zwaarder in de parameterbepaling. Indien gekeken wordt naar de relatieve afwijkingen ten opzichte van de berekende waarde, krijgen de metingen van weinig verbruik en lage belasting meer gewicht in de parameterbepaling. Deze methode maakt gebruik van vergelijking 3.36.

Uit de formule van Velander volgt:

[

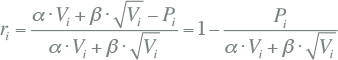
3.36

]

waarbij:

Pi	gemeten maximale belasting (kW)
Vi	gemeten jaarverbruik (kWh)
α, β	vast te stellen parameters
ri	residu van meting i

Van deze formule zijn niet eenvoudig de residuvergelijkingen op te stellen, waardoor de methode van oplossen met behulp van de normaalvergelijkingen van Gauss (vergelijkingen 3.29 tot en met 3.34) niet kan worden toegepast. Wel is het eenvoudig mogelijk met behulp van variatie van de parameters α en β in een computerprogramma de kleinste som van de kwadraten van de residuen r_i vast te stellen. Met behulp van deze ‘experimentele methode’ wordt voor de meetgegevens uit een steekproef: α = 0,20·10^-3 en β = 0,09. Toepassen van deze waarden leidt tot een te lage ligging van de curve voor de hoge vermogens. De kleinste kwadratenmethode leidt immers tot een curve, waarbij de meetpunten afwijkingen naar boven en naar beneden hebben. Het experimentele karakter van deze methode laat vrij om de parameters zodanig te beïnvloeden dat de curve voor zowel de grote vermogens als de lage vermogens niet teveel onder de waarden van de metingen ligt. Een betere afstemming wordt gevonden na aanpassen van de parameters: α = 0,22·10^-3 en β = 0,10.

De afbeeldingen in figuur 3.21 tonen in één grafiek de meetpunten, de curve volgens de parameterbepaling (die voorkeur geeft aan de grote vermogens) en de curve volgens de experimenteel geschatte parameters.

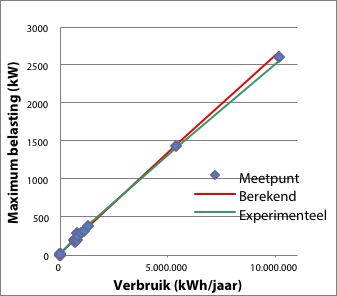
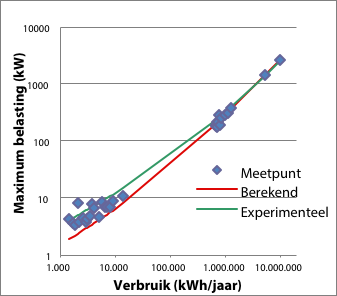
Figuur 3.21 Variatie van parameters α en β, afgebeeld met lineaire en dubbel-logaritmische schaalverdeling

3.6 Nieuwe ontwikkelingen

In het kader van het verduurzamen van de maatschappij en de daarbij in gang gezette energietransitie wordt gezocht naar alternatieven voor het gebruik van energie. Voorbeelden zijn te vinden in het gebruik van elektrische energie als alternatief voor andere energiedragers, zoals de elektrische auto en ruimteverwarming met behulp van warmtepompen en elektrische bijverwarming. Een ander voorbeeld is de alternatieve manier van opwekken van elektrische energie met behulp van windturbines, micro-WKK’s en zonne-energiesystemen (PV).

Een nadeel van deze ontwikkelingen is dat zij verantwoordelijk zijn voor een forse toename van het elektriciteitstransport over het distributienet en dat dit met een zeer grote waarde voor de gelijktijdigheid gepaard gaat. In netten waar deze nieuwe ontwikkelingen worden toegepast kan daarom niet meer alleen met het gedeelte van de belasting worden gerekend dat zich ongelijktijdig gedraagt maar moet ook rekening gehouden worden met een nieuwe component van de belasting die zich met een grote gelijktijdigheid gedraagt. Zo zullen nagenoeg alle elektrische auto’s worden opgeladen bij thuiskomst aan het einde van een werkdag en zullen warmtepompen met eventueel bijverwarming op koude dagen alle gelijktijdig in bedrijf zijn. Als gevolg hiervan zal in het ontwerp van het net (zowel bestaand als nieuw) in toenemende mate rekening moeten worden gehouden met de som van de individuele maximale belastingen.

3.6.1 Warmtepompen

In een groeiend aantal nieuwbouwprojecten worden woningen uitgerust met warmtepompsystemen voor verwarming en koeling. In de huidige nieuwbouw wordt in 6% van de woningen een warmtepomp toegepast, wat overeenkomt met de implementatie van 3500 warmtepompen per jaar. Vooralsnog zijn dit voornamelijk elektrische warmtepompen. Het werkingsprincipe is vergelijkbaar met dat van een koelkast of airconditioner. Voor het verwarmen van een ruimte wordt warmte onttrokken aan een medium. Dit medium kan de buitenlucht zijn of grondwater. Het voordeel van deze systemen is dat ze twee kanten op kunnen werken. Dat betekent dat een ruimte ook gekoeld kan worden door warmte af te geven aan het zelfde medium. Bij gebruik van grondwater als medium kan in de zomer warmte worden opgeslagen in de bodem, die er in de winter voor verwarmingsdoeleinden weer aan onttrokken wordt. Deze warmtepompsystemen zijn weliswaar energiezuiniger dan traditionele verwarmingsketels, maar verbruiken desalniettemin een forse hoeveelheid elektrische energie. De elektrische vermogens variëren van 2 tot 5 kW. Daarnaast is de warmtepomp veelal uitgerust met een bijverwarming met een vermogen van circa 6 kW, die in kan komen bij lage buitentemperatuur en na een langdurige storing van het elektriciteitsnet. Lage buitentemperatuur en een storing treffen alle woningen tegelijkertijd. Daarom moet bij grootschalige toepassing van warmtepompen in woningen terdege rekening gehouden worden met het feit dat deze apparaten een grote gelijktijdigheid vertonen in de elektriciteitsvraag. Hierbij geldt dat deze voornamelijk wordt bepaald door de warmtevraag in de winter of vraag naar koeling in de zomer. Met name in de winterperiode stijgt de behoefte naar ruimteverwarming aan het einde van de middag en in de avond gelijktijdig voor alle woningen. Ook op het warmst van een zomerdag zal de behoefte aan ruimtekoeling gelijktijdig stijgen. Het werkelijke gedrag is afhankelijk van de isolatiegraad van de woning. Bij goed geïsoleerde huizen zal het elektriciteitsprofiel van de warmtepomp vrijwel vlak gaan lopen.

Er zijn voorbeelden dat door een wijziging van het milieubeleid tijdens een nieuwbouwproject de woningen niet met conventionele verwarming maar met warmtepompen worden uitgevoerd. Als gevolg van de toegenomen elektriciteitsvraag bleek het distributienet niet meer voldoende. Het is dus van groot belang met de mogelijkheid van deze vorm van verwarming rekening te houden.

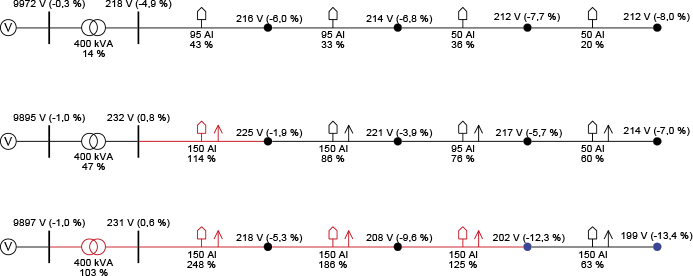
In projecten waar deze systemen worden toegepast zal de methode van Velander niet zonder meer gebruikt kunnen worden maar zal rekening gehouden moeten worden met gelijktijdige inschakeling van bijna alle warmtepompen. Dit veelal inclusief de bijverwarming en naast de gebruikelijke kleinschalige belasting. Dit houdt in dat de totale belasting wordt gesplitst in een deel met grote gelijktijdigheid en een deel met kleine gelijktijdigheid. Figuur 3.22 toont een gedeelte van een laagspanningsnet met 4 secties met elk 10 vrijstaande woningen, zonder warmtepompen (boven), met warmtepompen (midden) en met warmtepompen en ingeschakelde bijverwarming (onder). Bij de berekening van de LS-voedingskabels is uitgegaan van een vermogen van 3 kW per warmtepomp en 6 kW per bijverwarming. In het geval zonder warmtepompen kan de LS-hoofdkabel met aluminium geleiders verjongd worden van 95 naar 50 mm² geleiderdoorsnede. In het geval met alleen warmtepompen zijn in de eerste twee secties kabels met 150 mm² geleiderdoorsnede toegepast en dan nog is de eerste sectie overbelast. In het geval met warmtepompen en ingeschakelde bijverwarming is het net met toepassing van 150 mm² Al-kabels zwaar overbelast en is de spanning aan het einde van de streng te laag. Een oplossing voor dit vraagstuk kan worden gevonden door minder aansluitingen op een streng toe te laten of te werken met parallelle kabels, ervan uitgaande dat er geen kabels worden toegepast met een grotere geleiderdoorsnede.

Indien de warmtepomp en de bijverwarming driefasig zijn aangesloten, levert dat een extra belasting per aansluiting van 9000 kVA / 3 / 235 V = 12,8 A per fase. Bij een gelijktijdigheid van 1 kan dit voor 10 aansluitingen gewoon met 10 vermenigvuldigd worden, resulterend in een extra belastingstroom van 128 A. Deze stroom wordt opgeteld bij de standaard belasting van 10 vrijstaande woningen van maximaal 24 A, resulterend in een totale belastingstroom van 128 + 24 = 152 A, zichtbaar in de laatste kabelsectie van figuur 3.22. Hieruit blijkt dat de impact van warmtepompsystemen (128 A) zo groot is dat de invloed van het stochastische gedrag van de overige belasting (24 A) nagenoeg verwaarloosd kan worden.

Figuur 3.22 LS-hoofdkabel zonder en met warmtepompsystemen

3.6.2 Elektrische auto

De elektrische auto is anno 2010 aan een langzame opmars begonnen. Bij een doorbraak wordt gevreesd dat de piekbelasting sprongsgewijs toeneemt. De prognoses van het aantal elektrische auto’s in Nederland in het jaar 2020 lopen sterk uiteen, van 200 000 tot meer dan 1 miljoen. Een kwart miljoen is al ambitieus, maar in principe haalbaar. Het effect hiervan zal het meest merkbaar zijn in de laagspanningsnetten, direct gevolgd door de middenspanningsnetten. In dit kader staat de netbeheerder voor een aantal onzekerheden. Onder andere: hoe kan bij de bestaande transportcapaciteit deze nieuwe ontwikkeling goed worden ingepast en hoe moeten nieuw te ontwerpen netten hierop voorbereid worden? Om deze vragen te kunnen beantwoorden moet eerst naar het te verwachten elektrische gedrag van de elektrische auto gekeken worden.

In 2007 reed een personenauto gemiddeld 13877 km in het jaar (CBS Statline). Aangenomen wordt dat het verbruik van de elektrische auto 5-7 km/kWh (gemiddeld 1 kWh op 6 km) is. Dit is gebaseerd op specificaties van leveranciers en op praktijkcijfers, die uiteenlopen van 1 op 4 tot 1 op 7, afhankelijk van rijstijl en type auto. Dat houdt in dat het jaarverbruik van een elektrische auto gelijk is aan 13877/6 = 2312 kWh/jr. Op basis van dit jaarverbruik komt dit neer op een verbruik van circa 6,3 kWh per dag. Ter vergelijking, het gemiddelde jaarverbruik van een woning in 2007 is 3512 kWh (9,6 kWh per dag).

De piekbelasting van een elektrische auto wordt bepaald door de hoeveelheid bij te laden energie en de tijdsduur van het laden. Voor het berekenen van de piekbelasting in de thuissituatie kan worden aangenomen dat een lege accu in een nacht opgeladen moet kunnen worden. Indien uitgegaan wordt van een duur van 8 uur (van 23:00 uur tot 7:00 uur) en een accucapaciteit in de auto van 16 tot 36 kWh (anno 2009), dan is het benodigde laadvermogen van een auto:

• Voor een kleine accu: 16 / 8 = 2 kW
• Voor een grote accu: 36 / 8 = 4,5 kW

Er zijn elektrische auto’s waarvan het piek-laadvermogen is afgestemd op een reguliere installatie van 10 A en 230 V, waardoor het piek-laadvermogen beperkt is tot 2 kW. Er zijn ook elektrische auto’s die zijn uitgerust met een krachtstroomstekker, die geschikt is voor 3 x 16 A en 400 V. Hiermee kan bij gebruik van een fase geladen worden met 3,5 kW en bij gebruik van drie fasen met 10 kW. De Europese standaardstekker is geschikt voor 3 x 63 A en 400 V. Dit zou overeenkomen met een piek-laadvermogen van 40 kW. Dit vermogen wordt nog niet geheel benut. De ontwikkelingen van de laders zijn in 2010 nog niet zover. Er zijn fabrikanten die nadenken over een lader van 20 kW. Als dit soort laders in grote hoeveelheden worden toegepast en als zij tegelijkertijd laden, zullen zij een probleem vormen ten aanzien van de piekbelasting van het distributienet.

Een vermogen van 4,5 kW voor het in 8 uren opladen van een grote accu kan al niet meer door een normaal stopcontact met een zekering van 16 A worden geleverd. In dat geval moet gebruik worden gemaakt van een driefasenaansluiting of moet genoegen worden genomen met een langere tijdsduur. Een tijdsduur van 10 uren betekent een laadvermogen van 3,6 kW en dit komt bij een spanning van 230 V overeen met een stroom van 15,7 A. Een voorwaarde is dat de oplaadcyclus voor elke elektrische auto, onafhankelijk van de laadtoestand van de accu, gespreid wordt over de maximale tijdsduur van 8 tot 10 uren. In aanmerking moet worden genomen dat in veel huishoudelijke situaties de oplaadtijd ook 12 uur zou mogen bedragen, hetgeen de piekbelasting zou kunnen reduceren. Figuur 3.23 illustreert de elektriciteitsvraag in geval van een niet gestuurde oplaadcyclus, waar de stroom in de avonduren gedurende korte tijd zeer groot is. Figuur 3.24 toont een situatie van een geoptimaliseerde oplaadcyclus, waarbij de tijdsduur door de klant is ingesteld. Het voorbeeld gaat uit van een wijk met 40 eengezinswoningen waarvan bij 25% van de woningen een elektrische auto opgeladen moet worden. Er zijn dus in dit voorbeeldnet 10 elektrische auto’s aanwezig, waarvan de energiebehoefte gemiddeld 6,3 kWh per dag is.

Bij een ongecontroleerde oplaadcyclus kan een gemiddelde energie van 6,3 kWh per auto in 2 uren geleverd worden bij een stroomsterkte van 13,7 A en een enkelfasige spanning van 230 V. In het voorbeeld is ervan uitgegaan dat de helft van de auto’s vanaf 19:00 uur wordt opgeladen en de andere helft vanaf 20:00 uur. Dit veroorzaakt in het eerste uur een extra stroomsterkte van 23 A per fase en in het tweede uur een extra stroomsterkte van 46 A per fase. Als dit in de avonduren tijdens de maximale belasting plaatsvindt, kan het net hierdoor overbelast raken.

Voorbeeld ongecontroleerd opladen:

• Aantal woningen: 40
• Aantal elektrische auto’s: 10
• Energiebehoefte: 6,3 kWh per auto gemiddeld
• Totale energiebehoefte: 63 kWh
• Aantal uren benodigd voor opladen: 2
• Piekvermogen: 63 kWh / 2 h = 31,5 kW
• Maximale stroom driefasensysteem: (31500/3) / 230 = 46 A/fase

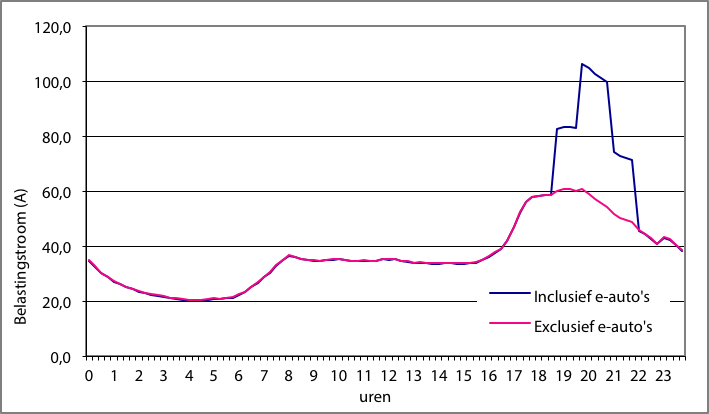
Figuur 3.23 Ongecontroleerde oplaadcyclus van 10 elektrische auto’s

Bij een gecontroleerde en geoptimaliseerde oplaadcyclus kan de gemiddelde energie van 6,3 kWh per auto in 8 uren gespreid geleverd worden bij een stroomsterkte van 3,4 A en een enkelfasige spanning van 230 V. In het voorbeeld is ervan uitgegaan dat alle auto’s vanaf 22:00 uur worden opgeladen. Dit veroorzaakt in het net een extra stroomvraag van 11,4 A per fase.

Voorbeeld gecontroleerd en geoptimaliseerd opladen:

• Aantal woningen: 40
• Aantal elektrische auto’s: 10
• Energiebehoefte: 6,3 kWh per auto gemiddeld
• Totale energiebehoefte: 63 kWh
• Aantal uren benodigd voor opladen: 8
• Piekvermogen: 63 kWh / 8 h = 7,9 kW
• Maximale stroom driefasensysteem: (7900/3) / 230 = 11,4 A/fase

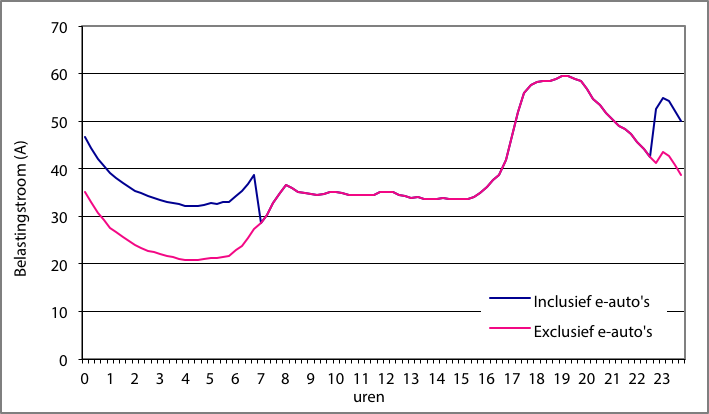
Figuur 3.24 Geoptimaliseerde oplaadcyclus van 10 elektrische auto’s

Bovenstaand voorbeeld illustreert het belang van de spreiding van de oplaadperiode van de elektrische auto’s. Ook belastingsturing voorkomt dat het opladen voor of tijdens de piek in de avonduren start.

Door de accu’s gestuurd op te laden (slim laden) wordt de vraag afgestemd op de netcapaciteit en eventueel op het aanbod van duurzame energie. De stromen waarbij accu’s geladen worden als ze aan het net gekoppeld zijn, mogen variëren gedurende de laadsessie. Hierbij worden de accu’s vanuit het net alleen opgeladen. De accu’s kunnen in principe ook gebruikt worden als buffer voor het net, waarbij zij elektriciteit terugleveren aan het net. Hierdoor zal het aantal op- en ontlaadcycli toenemen Een nadeel dat hierbij optreedt is dat dit tot snellere slijtage van de accu’s kan leiden. Daarom zal dit maar met mate worden toegepast.

Er wordt geëxperimenteerd met snelladen binnen 20 tot 40 minuten. Snelladen betekent in de praktijk het opladen van de accu van 20% lading naar 80% lading, dus niet van 0 naar 100%. Wel treedt hier, door de grote vermogens veel warmteverlies op. Daarom is het laadvermogen al snel 10% of meer groter dan het vermogen dat in de accu komt. Voor het 60% opladen binnen een half uur is dan het benodigde laadvermogen, inclusief de warmteverliezen, per auto:

• Voor een kleine accu: 0,6 · ( 16 / 0,5 ) · 1,1 = 21 kW
• Voor een grote accu: 0,6 · ( 36 / 0,5 ) · 1,1 = 48 kW

Deze vermogens corresponderen in een LS-driefasensysteem met een stroomsterkte van respectievelijk 30 en 70 A, uitgaande van een arbeidsfactor van 1. Aanleg van een faciliteit om meerdere auto’s te kunnen snelladen vergt een specifieke investering in de infrastructuur. Vanwege de hierbij optredende hoge stroomvraag kan dit eventueel leiden tot een eigen MS-aansluiting of een distributiestation.

Voor het berekenen van de gelijktijdigheid voor het laden van veel auto’s in de woonsituatie kan worden uitgegaan van het gemiddelde elektriciteitsverbruik van een auto van 6,3 kWh/dag. De gelijktijdige belasting van het net door ’s nachts gedurende 8 uren te laden wordt dan 6,3 kWh gedeeld door 8 = 0,79 kW per elektrische auto (gebaseerd op gegevens van een elektrische auto in 2010). Het probleem met de gelijktijdigheid is dat er nog helemaal geen ervaring is opgedaan met het grootschalig opladen van elektrische auto’s. In het ergste geval is de gelijktijdigheidsfactor 1, waardoor alle piek-laadvermogens gelijktijdig zijn aangesloten. Dit betekent dat de extra piekbelasting kan liggen tussen 0,79 kW per auto en 10 kW per auto, bij de stand van de toegepaste techniek in 2010.

Het rekenen met gelijktijdigheid gaat altijd uit van grote aantallen. Het aantal elektrische auto’s is vooralsnog gering. Bovendien blijkt de diversiteit van de behoefte om op te laden groot. Ook kan rekening gehouden worden met de mogelijkheid om ook overdag, in parkeergelegenheden bij winkelcentra of op het werk, de accu’s van de auto’s op te laden. Met name het grote aantal elektrische auto’s kan leiden tot een grote, tot op heden niet voorziene, toename van de belasting lokaal in het netwerk.

3.7 Decentrale opwekking

Decentrale opwekking is allang niet meer een marginaal verschijnsel in de distributienetten. De toegepaste systemen variëren van micro-WKK’s en PV-systemen in laagspanningsnetten tot aan grote WKK- en windenergiesystemen die op het middenspannings- en hoogspanningsnet worden aangesloten. Windturbines met elk een vermogen van 3 tot 5 MW, verzameld in windparken, voeden in op transportnetten op middenspannings- of hoogspanningsniveau. In warmtekrachtcentrales worden grote generatoren toegepast die, afhankelijk van hun vermogen, op het distributie- dan wel het transportnet zijn aangesloten. Maar ook grote hoeveelheden kleine generatoren, zoals in micro-WKK installaties, worden in toenemende mate in de LS-netten toegepast. Deze zijn meestal via converters aangesloten.

Er worden in de literatuur uiteenlopende definities voor decentrale opwekking gehanteerd. De meeste definities zijn gebaseerd op het type technologie dat toegepast wordt, de impact op het milieu van de installatie, de grootte van het opgesteld vermogen van de installatie en het spanningsniveau waaraan de installatie is gekoppeld. Een definitie op basis van type technologie is lastig vanwege de grote diversiteit aan technologische ontwikkelingen, zoals WKK-systemen, PV-systemen en windmolens. Een definitie op basis van het spanningsniveau of op basis van de grootte van het opgesteld vermogen wordt ook wel gebruikt. De NMa hanteert geen specifieke definitie van decentrale opwekking, maar spreekt over (NMa 2009_2):

• productiemiddel: een (deel van een) installatie bestemd voor het opwekken van elektriciteit, bestaande uit één of meer productie-eenheden
• productie-eenheid: een (deel van een) productiemiddel, dat zelfstandig (ofwel onafhankelijk van de andere delen van het desbetreffende productiemiddel) kan worden ingezet voor het opwekken van elektriciteit. Van een productie-eenheid kunnen één of meer generatoren deel uitmaken.

Daarnaast hanteert de NMa de term ‘duurzame elektriciteit’, die wordt opgewekt met hernieuwbare energiebronnen, zoals wind, zonne-energie, aardwarmte, golfenergie, getijdenenergie, waterkracht, biomassa, stortgas, rioolwaterzuiveringsgas en biogas (Elektriciteitswet 1998). Een groot gedeelte van de decentrale opwekking valt onder de noemer van duurzame elektriciteit. De productie van duurzame elektriciteit is gestegen van 6,0 procent van het binnenlands elektriciteitsverbruik in 2007 tot 7,5 procent in 2008. Dit komt door een toename van de elektriciteitsproductie uit windenergie en biomassa.

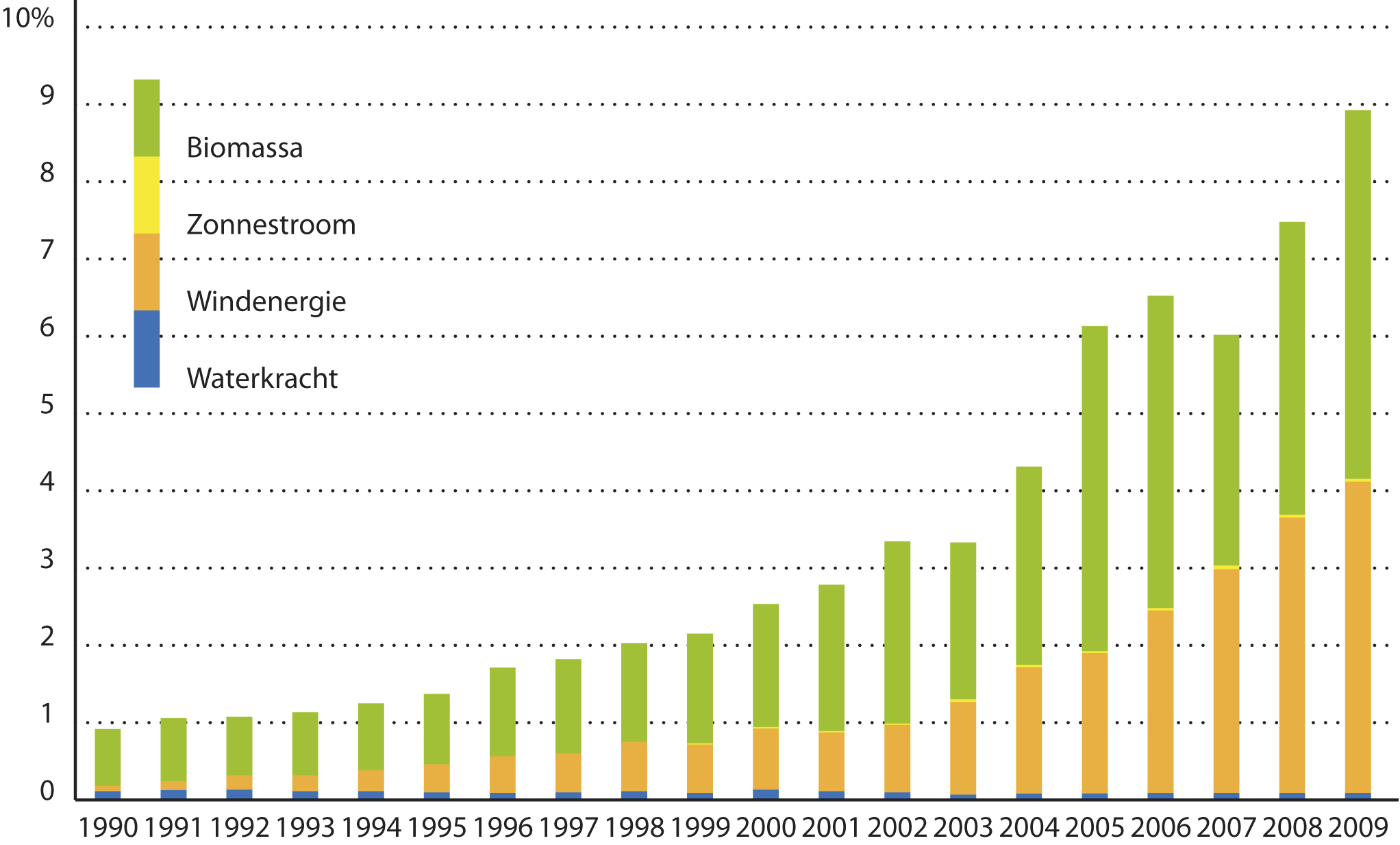
Figuur 3.25 Ontwikkeling van duurzame elektriciteit in Nederland (bron: CBS)

De elektriciteitsproductie uit windenergie was in 2008 een kwart hoger dan in 2007. Dit komt vooral doordat er veel nieuwe windmolens in gebruik zijn genomen. Windenergie is daarmee verantwoordelijk voor ongeveer de helft van de duurzame elektriciteitsproductie. Eind 2008 was de windmolencapaciteit 2216 megawatt, ongeveer 470 MW meer dan een jaar eerder (CBS, 2009).

De generatoren van decentrale opwekkers zijn meestal uitgevoerd als synchrone machine en soms als asynchrone machine. Een synchrone generator heeft een rotor die zodanig bekrachtigd is dat deze zich gedraagt als een roterende magneet. De rotor draait in het elektromagnetische veld dat wordt opgewekt door de statorwikkelingen die op het elektriciteitsnet zijn aangesloten. Hierdoor is de synchrone machine gedwongen synchroon met het door het net bepaalde roterende veld mee te draaien. De frequentie van de spanning die door de synchrone generator wordt opgewekt moet 50 Hz bedragen. Een asynchrone generator heeft daarentegen een kortgesloten rotorwikkeling, waarin een stroom loopt waarvan de grootte en frequentie afhangen van het verschil in omwentelingsnelheid van de rotor ten opzichte van het ronddraaiende elektromagnetische veld van de statorwikkelingen. De asynchrone generator kan alleen vermogen opwekken indien hij sneller (dus asynchroon) dan het door het net bepaalde roterende veld draait.

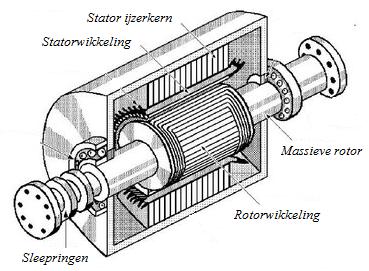
Figuur 3.26 Synchrone generator voor groot vermogen

Decentrale opwekking heeft invloed op het gedrag van stromen en spanningen in het distributienet. In het algemeen veroorzaakt een generator een stijging van de spanning en een toename van het kortsluitvermogen. Soms kan dit wenselijk zijn, maar soms niet. Een loadflow- en kortsluitberekening geeft hier meer inzicht in. Hierop wordt in de hoofdstukken 9 en 10 verder ingegaan. De maximale kortsluitstroom van via converters aangesloten generatoren is door de elektronica beperkt tot ongeveer de nominale stroom. Onderstaande systemen worden in de distributienetten en MS-transportnetten het meest toegepast.

• Micro-WKK-systemen: 1 .. 5 kW per aansluiting
• PV-systemen: 0,5 .. 2 kW per aansluiting
• Windturbines: 1 .. 5 MW per aansluiting
• WKK-systemen bij tuinders: 100 .. 630 kW per aansluiting
• Grote WKK-systemen: 1 .. 20 MW per aansluiting

Grotere windturbines met een vermogen van 5 MW of meer en grote WKK-installaties kunnen niet zonder meer in het net worden opgenomen. Een nadere studie en een berekening van de effecten die gepaard gaan met het al dan niet leveren van elektrische energie aan het net en de gevolgen van kortsluiting in het net, moeten hierbij vooraf zijn uitgevoerd.

3.7.1 Micro-WKK-systemen

In een groeiende hoeveelheid nieuwbouwprojecten worden woningen uitgerust met micro-WKK systemen. Deze systemen kunnen een relatief klein vermogen van 1 tot 5 kW per aansluiting leveren. De gelijktijdigheid van deze systemen is vrij groot. De elektriciteitsproductie volgt immers de warmtevraag. Die hangt af van het bewonerspatroon. Bij een relatief grote groep gelijksoortige woningen kan verwacht worden dat de warmtevraag gemiddeld genomen ook gelijksoortig is. Zo zullen bijvoorbeeld de meeste werkenden omstreeks 18:00 uur thuiskomen en zal tijdens koude dagen op dat moment de warmtevraag in woningen toenemen. Bij niet-werkenden zal de warmtevraag over de hele dag genomen minder sterk variëren. Het voordeel van deze vorm van decentrale opwekking is dat de meeste productie van elektriciteit grotendeels samenvalt met de vraag. Met name in de wintermaanden is de normale belasting van woonwijken in de avonduren vrij groot, zoals geïllustreerd in figuur 3.4. Als gevolg zal de netto belasting van een distributienet door de micro-WKK systemen afnemen. Het gedrag van de aangeslotenen is echter onzeker, zodat voor het verlagen van de piek uitgegaan mag worden van een schatting van de minimum opbrengst van de micro-WKK systemen.

In de laagspanningsnetten worden éénfase micro-WKK’s toegepast. Dit zijn voor netberekeningen redelijk eenvoudige componenten, die een specifiek gedrag vertonen in geval van starten en bij kortsluiting. Omdat de verwachting is dat deze opwekkers in de toekomst veelvuldig zullen worden toegepast, is het belangrijk om juist aan dit soort componenten specifiek aandacht te besteden. Met name het collectieve gedrag tijdens kortsluitingen en het gelijktijdig starten na herstel van de elektriciteitsvoorziening is onderwerp van studie in (toekomstige) projecten.

Veel micro-WKK’s zijn uitgerust met een Stirlingmotor. Bij een Stirling machine vindt de verbranding van de brandstof buiten de motor plaats. Het arbeidsmedium, bijvoorbeeld lucht of helium, dat zich in de machine bevindt, verlaat deze nooit. De motor bestaat uit een koud deel en een warm deel. Deze zijn in figuur 3.27 aangegeven met blauw en rood. Een warmtebron, bijvoorbeeld de vlam van een gasbrander, of hete gassen van een verwarmingsketel, verwarmt voortdurend het warme deel van de motor terwijl het koude deel continu gekoeld wordt door bijvoorbeeld het retourcircuit van de verwarming. Beide delen, warm en koud, staan voortdurend met elkaar in verbinding. Het arbeidsmedium wordt door een verplaatser (bijna) zonder arbeid heen en weer geschoven tussen de hete en de koude ruimte, waarbij het medium in de hete ruimte onder het opnemen van warmte expandeert en arbeid verricht door een zuiger te bewegen. Vervolgens wordt de lucht door de verplaatser weer naar de koude ruimte bewogen, koelt daar af en neemt in volume af. Het arbeidsmedium, opgesloten in de motor, circuleert dus voortdurend van het warme naar het koude deel en omgekeerd en beweegt hierbij de zuiger heen en weer. De zuiger kan een lineaire generator aandrijven of via een overbrenging een meer conventionele roterende generator.

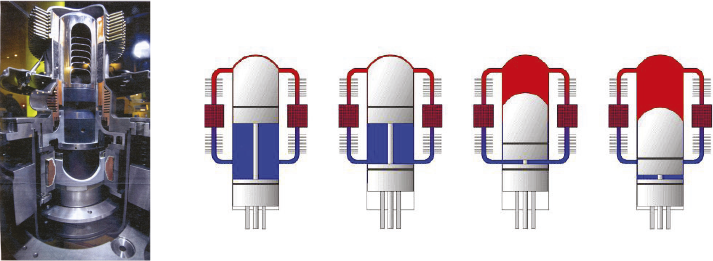
Figuur 3.27 Voorbeeld van een opengewerkte Stirlingmachine en het werkingsprincipe

Er zijn twee varianten voor de elektriciteitsopwekking in de micro-WKK’s.

• Het type Microgen is voorzien van een lineaire synchrone generator.
• Het type WhisperGen is voorzien van een gemodificeerde kortsluitanker­generator.

Microgen

Deze generator is geen roterende machine. Het elektrische vermogen wordt opgewekt door een lineair trillende magneet, die via de zuiger van de Stirlingmachine wordt aangedreven. De generator is via een converter aan het net gekoppeld.

WhisperGen

De WhisperGen-WKK maakt gebruik van een gemodificeerde asynchrone generator die, via een overbrenging, door vier zuigers van de Stirlingmachine wordt aangedreven. De stator van de kleine asynchrone motor is gewikkeld als een 4-polige tweefasengenerator. De stroom in de hulpwikkeling is met behulp van een condensator 90 graden verschoven om een draaiveld te genereren. Figuur 3.28 illustreert dit aan de hand van het wikkelschema voor de stator. De hoofdwikkeling is met blauw aangegeven en de hulpwikkeling met rood.

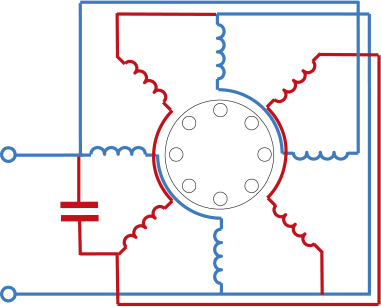
Figuur 3.28 Rotor en stator van gemodificeerde asynchrone generator

3.7.2 PV-systemen

Zonlicht wordt met fotovoltaïsche cellen in zonnepanelen omgezet in gelijkspanning. Via een converter worden de zonnepanelen voor de vermogensoverdracht aan het net gekoppeld. Zonnepanelen hebben met de stand van de techniek in 2010 een vermogen van 100 tot 120 W per m². In praktische situaties leidt dit tot vermogens van 0,5 tot 2 kW per aansluiting. Figuur 3.29 toont een PV systeem met 112 panelen. Deze zijn tezamen goed voor ruim 10 kW. Bij grootschalige toepassing kunnen deze PV-systemen op zomerse dagen zoveel elektriciteit produceren dat tijdens momenten van lage belasting de energievraag wijzigt in een energieoverschot, waardoor de energierichting in een LS-net omkeert.

De gelijktijdigheid van de elektriciteitsopbrengst van PV-systemen in een LS-distributienet is groot, vanwege de verhouding van het gebied dat de effecten van bewolking ondervindt tot de grootte van het gebied dat een distributiestation verzorgt. Een gelijktijdigheidsfactor van 1 kan gerust gebruikt worden voor het plannen van LS-distributienetten. Het verzorgingsgebied van een voedingsstation bestrijkt een vele malen groter gebied, waardoor de gelijktijdigheid van alle PV-systemen in geval van bewolking afneemt. Echter, tijdens een onbewolkte dag zullen alle PV-systemen maximaal produceren, zodat ook op de schaal van een MS-distributienet gerekend kan worden met een gelijktijdigheidsfactor van 1. De studies naar de invloeden van PV-systemen zullen zich voornamelijk afspelen op het vlak van de lokale LS-distributienetten. Hierbij zal met name gekeken worden naar de combinatie van maximale opbrengst en minimale belasting.

Figuur 3.29 10 kW PV-systeem op een boerderij

Figuur 3.30 Converters voor 20 kW PV-systeem

De PV-systemen zijn altijd aangesloten via een omvormer. Figuur 3.30 toont een systeem met drie converters voor een totaal vermogen van 20 kW. De PV-panelen leveren een gelijkspanning van ongeveer 40 tot 50 V, die moet worden geconverteerd. Hierdoor is het kortsluitvermogen altijd beperkt tot maximaal de nominale stroom van de omvormers. Een PV-systeem levert alleen vermogen wanneer het systeem aangesloten is op het 230 V distributienet. Ingeval van een storing stopt de converter met de productie. Dit is een veiligheidseis.

3.7.3 Windturbines

Windturbines hebben een nominaal vermogen van 1 tot 5 MW per windmolen. Meestal worden ze in windparken geclusterd in kleine tot vrij grote groepen. In het verleden werden deze windparken alleen op land geplaatst, maar steeds vaker worden grote windparken op zee aangelegd. Het potentieel voor de opbrengst van windenergie op zee wordt geschat op twee maal het totale Nederlandse energieverbruik.

Het vermogen van een enkele windturbine is te groot om op een laagspanningsnet te worden aangesloten. Een vermogen van 1 MW leidt in een LS-net al tot een stroom van 1,4 kA. Om deze reden worden windturbines op MS-niveau aangesloten. Grote windparken worden op HS-niveau aangesloten.

Er bestaan windturbines voor constant en voor variabel toerental. Bij windturbines met een vast toerental is de generator (een asynchrone machine) direct gekoppeld aan het net. Bij deze windturbines is elke fluctuatie in de windsnelheid direct merkbaar in het actieve vermogen. Windturbines met een variabel toerental worden geregeld met behulp van vermogenselektronica, waardoor fluctuaties in windsnelheid voor een groot deel kunnen worden opgeslagen in rotatie-energie van de rotor. Dit laatste zorgt ervoor dat bij windturbines met variabel toerental de geleverde energie weinig fluctuaties vertoont.

De nieuwe grote generatoren zijn meestal van het type DFIG (Doubly Fed Induction Generator), waarvan de statorwikkeling direct op het net is aangesloten en de rotorwikkeling via een converter. Door de frequentie van de stroom door de rotorwikkeling te variëren kan deze synchrone generator bij variabel toerental functioneren. Dit type windturbine en zijn gedrag is goed beschreven in de literatuur (Slootweg, 2003). Deze generatoren worden ingezet in windturbines voor vermogens tussen 1 en 5 MW.

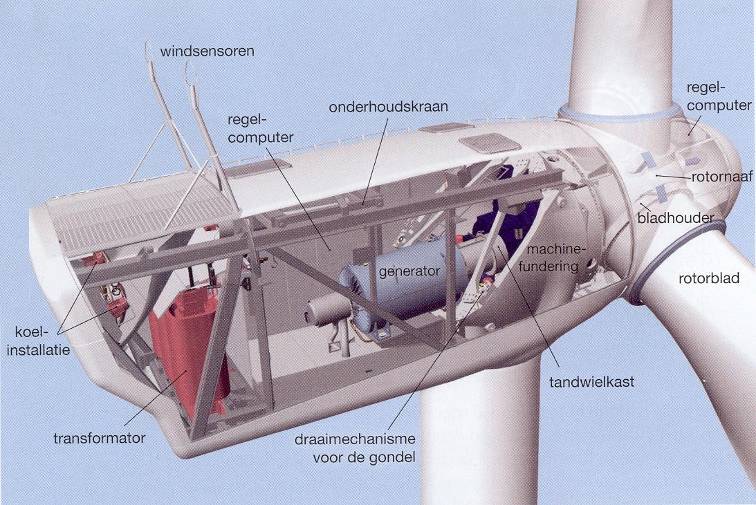
Figuur 3.31 Opengewerkte windturbinegondel

Voor het vaststellen van de te verwachten elektriciteitsproductie is inzicht in de vermogenskarakteristiek van belang. De vermogenskarakteristiek van elke windturbine is zodanig dat beneden de cut-in windsnelheid het vermogen nul is. Boven deze windsnelheid is het elektrisch vermogen afhankelijk van de derde macht van de windsnelheid. Boven de nominale windsnelheid is het vermogen constant en gelijk aan het nominale vermogen. Boven de cut-out windsnelheid wordt de windturbine buiten bedrijf genomen om beschadigingen te voorkomen.

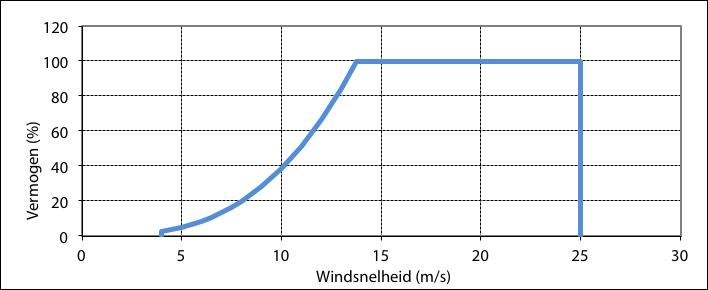
Figuur 3.32 Vermogenskarakteristiek van een windturbine

3.7.4 Grote WKK-systemen

Een WKK-systeem wordt geplaatst om warmte, meestal met een hoge temperatuur te produceren. Deze warmte wordt gebruikt in de industrie, voor ruimteverwarming, in de tuinbouw of voor stadsverwarming. De WKK produceert hiervoor stoom of heet water en de restwarmte wordt gebruikt voor het opwekken van elektriciteit, die eventueel teruggeleverd wordt in het net. Door de gecombineerde opwekking in het WKK-systeem kan een hoog energetisch rendement worden behaald.

Sinds 2006 is vooral in de glastuinbouw de elektriciteitsproductie sterk gestegen. Veel glastuinbouwbedrijven gebruiken een gasmotor voor de opwekking van elektriciteit en warmte. Hiermee verlichten en verwarmen ze hun kassen. Vanwege de hoogte van de energieprijzen is de verkoop van elektriciteit een aantrekkelijke extra inkomstenbron voor deze tuinders. Er zijn dan ook veel nieuwe gasmotoren geïnstalleerd, waardoor het elektrisch vermogen in deze sector in twee jaar tijd is verdubbeld. Aan het begin van 2008 bestond ruim 10 procent van het totale elektrische vermogen in Nederland uit productie-eenheden in de glastuinbouw (CBS, 2009). Inmiddels daalt dit percentage weer door de toename van conventionele centrales en WKK-centrales.

Door de toename van de hoeveelheid decentrale opwekking met grote WKK-installaties kan de belasting van het MS-distributienet aanzienlijk veranderen. De gevolgen zijn sterk afhankelijk van de specifieke locatie in het net. Het is mogelijk dat het distributienet niet berekend is op veel decentrale invoeding. De richting van de vermogensstroom, traditioneel van een hoog naar een laag spanningsniveau, kan omkeren. Dit kan leiden tot minder of juist extra netkosten. Netverliezen kunnen toenemen, doordat de afstand van de opwekinstallatie tot de afnemer toe kan nemen, bijvoorbeeld als veel opwekkers in een perifere regio worden opgesteld. Aan de andere kant kunnen netverliezen afnemen doordat het elektrische vermogen dichter bij de verbruiker wordt opgewekt.

De elektrische vermogens van WKK-installaties liggen in de ordegrootte van 0,1 tot 20 MW per aansluiting. Grotere vermogens komen ook voor. Een 10 kV-kabel met een aluminium geleider van 240 mm² mag belast worden met 5 MVA. Een vermogen van 20 MW is dan ook teveel om op het MS-distributienet aan te sluiten. Figuur 3.6 en figuur 3.7 illustreren metingen van voedingsstromen van 20 kV-strengen in kassengebieden. De patronen vertonen dagelijkse belastingschommelingen tot 17 MW tussen maximale vraag en aanbod. Deze schommelingen worden veroorzaakt door de som van de patronen van de belasting en van de opwekking. Met name in de glastuinbouw worden WKK-eenheden met vermogens van 3 tot 4 MW geclusterd. In tuindersgebieden komen clusters voor met vermogens tot 100 MW, die aangesloten zijn op het HS-net. De grootte van een complete installatie wordt dan mede bepaald door de omvang van het betreffende kassengebied.

Tuinders produceren niet alleen elektriciteit naar de eigen warmte- en elektriciteitsbehoefte maar ook volgens de marktvraag naar elektrische energie. Bij een hoge kWh-prijs kunnen zij extra elektriciteit produceren en bij een lage kWh-prijs kunnen zij zelfs elektriciteit inkopen. Het is niet zozeer een energietechnische maar een economische afweging. De maximale elektriciteitsproductie hoeft dus niet samen te vallen met de maximale lokale elektriciteitsvaag. Voor het aansluiten van dergelijke grote installaties moet daarom altijd een gedegen studie worden uitgevoerd, waarbij uitgegaan wordt van de extreme situaties van maximale opwekking tegelijk met minimale belasting en minimale opwekking tegelijk met maximale belasting. De capaciteit van het MS-net is beperkt, zodat voor het aansluiten van een groot cluster in veel gevallen een netverzwaring nodig is. In extreme gevallen is zelfs verzwaring van het HS-net nodig.

3.8 Motoren

Motoren worden veelvuldig toegepast in de industrie en vormen daar het grootste deel van de belasting. Bij het dimensioneren van industriële netten moet terdege rekening gehouden worden met het gedrag van de motoren. Met name bij het starten van de motor en bij het optreden van een kortsluiting in het net is de invloed van de motor merkbaar. Het starten van een motor vraagt kortstondig een grote stroom van 4 tot 8 maal de nominale stroom, hetgeen leidt tot een spanningsdip. Deze aanloopstroom kan worden beperkt door het toepassen van een sterdriehoek schakeling, een softstarter of een frequentieomvormer. Indien een motor wordt bestuurd met behulp van vermogenselektronica, kan dit leiden tot toename van de harmonische vervorming van de wisselspanning. Indien een kortsluiting in het net optreedt, zullen de motoren bijdragen aan de kortsluitstroom waardoor deze op de kortsluitplaats vergroot wordt. De invloed van motoren is in de meeste distributienetten gering. In een situatie dat in een industriële omgeving vele en grote motoren zijn toegepast, kan het echter nodig zijn hun invloed op het net nader te bestuderen.

Wisselstroommotoren bestaan in de uitvoeringsvormen van de synchrone en de asynchrone machine. De synchrone motor heeft dezelfde constructie als de synchrone generator. Grote synchrone motoren worden bijna uitsluitend in de industrie toegepast. De asynchrone motor heeft een kortgesloten rotorwikkeling. Deze motoren worden ook wel inductiemotor of kortsluitankermotor genoemd. Bij nullast draait de asynchrone motor iets langzamer dan het synchrone toerental. Indien de motor wordt belast, zal hij nog iets langzamer gaan lopen. Dit gedrag is vastgelegd in de koppel-toerenkromme van de motor. Bij toename van de belasting zal de motor een punt bereiken waarbij de motor het gevraagde koppel niet meer kan leveren. De motor zal dan tot stilstand komen. Het punt waarop dit gebeurt, wordt aangeduid met het kippkoppel. Bij stilstand zal de motor een stroom trekken die gelijk is aan de aanloopstroom.

Figuur 3.33 Asynchrone machine

Motoren kunnen direct op het net (DOL, Direct On Line) zijn aangesloten. In dat geval moet rekening gehouden worden met de grootste aanloopstroom. Om de aanloopstroom te beperken kunnen de wikkelingen bij sommige uitvoeringen tijdelijk van driehoek naar ster worden geschakeld. Hierbij krijgen de wikkelingen tijdens het aanlopen een spanning die een factor √3 lager is dan normaal. Motoren kunnen ook met behulp van een softstarter aanlopen. Hiermee wordt de aanloopstroom beperkt tot ongeveer de nominale stroom. Motoren waarvan het toerental geregeld wordt, zijn via een frequentieomvormer op het net aangesloten. Deze converters beperken de aanloopstroom tot ongeveer de nominale stroom.

Asynchrone motoren leveren in geval van kortsluiting in het net een kortstondige bijdrage aan de kortsluitstroom, die ongeveer gelijk is aan de aanloopstroom. Motoren die via een frequentieomvormer zijn aangesloten leveren in de regel geen bijdrage aan de kortsluitstroom. In het geval dat de frequentieomvormer teruglevering mogelijk maakt is de kortsluitstroombijdrage beperkt tot ongeveer de nominale stroom.

Motorbesturing	Aanloopstroom	Kortsluitstroombijdrage
Direct op het net	6 .. 8 x nominale stroom	6 .. 8 x nominale stroom
Softstarter	ongeveer nominale stroom	6 .. 8 x nominale stroom
Converter	ongeveer nominale stroom	geen bijdrage of ongeveer nominale stroom

3.9 Onderscheid problematiek op MS- en LS-niveau

Op laagspanningsniveau worden de netten meestal gekarakteriseerd door grote aantallen kleine afnemers. Het is meestal gerechtvaardigd om over afnemers te spreken omdat zij voornamelijk elektriciteit verbruiken. De voorzieningsgebieden op LS-niveau zijn meestal van dien aard dat de afnemers een voorspelbaar en gelijksoortig karakter hebben. Het is daarom gebruikelijk om te werken met specifieke belastingstypen en gebruik te maken van de gelijktijdigheid van de afnemers. Ook indien de gebruikers zelf elektriciteit opwekken met behulp van bijvoorbeeld PV-systemen, is het nog gerechtvaardigd om op deze manier te werken.

Bij introductie van grote elektriciteitsverbruikers, zoals de elektrische auto en ruimteverwarming met behulp van warmtepompen en elektrische bijverwarming, volstaat het niet meer om rekening te houden met de ongelijktijdigheid van de elektriciteitsvraag van alle afnemers en moet rekening gehouden worden met het feit dat grote elektriciteitsverbruikers gelijktijdig in bedrijf zijn. Ten aanzien van de toekomstige ontwikkelingen zijn de onzekerheden het grootst in de laagspanningsnetten. Als gevolg hiervan zal bij nieuwbouw van netten steeds meer ontworpen worden op basis van de som van de individuele maximale belastingen. Hierom ontstaat de trend dat de netontwerper zich steeds meer gaat indekken voor deze toekomstige onzekerheden en zal hij het laagspanningsnet zo zwaar mogelijk gaan ontwerpen: met maximale kabeldoorsneden, van bijvoorbeeld 150 mm² aluminium geleider, en een zo groot mogelijke distributietransformator, van bijvoorbeeld 630 kVA. Ook zal de netontwerper bij nieuwbouw extra ruimte claimen om in de toekomst, mocht het nodig blijken, extra netruimten te kunnen plaatsen en zo toekomstige kosten zoveel mogelijk te vermijden.

Op MS-niveau moet goed worden gerealiseerd of het net aansluitingen bedient die een afwijkend gedrag vertonen. Naast de distributiestations, die grote groepen laagspanningsklanten bedienen, komen namelijk ook kleine hoeveelheden aansluitingen van grote vermogens voor, die als functie van de tijd een afwijkend belastingspatroon vertonen. Met name de decentrale opwekking op MS-niveau vertoont een gedrag dat niet eenvoudig met gelijktijdigheidsfactoren te modelleren is. Indien het gedrag van de belasting op opwekking van een grote klant goed bekend is, kan met belastingspatronen worden gewerkt. Er wordt dan meer specifiek gekeken naar de belasting en opwekking in de loop van een bepaalde periode. Het net moet dan voor alle situaties geschikt zijn voor de te distribueren vermogens. Indien het gedrag onbekend is en niet betrouwbaar vastgesteld kan worden, kan alleen worden volstaan door rekening te houden met extreme situaties in opwekking en belasting. In dat geval moet bij het analyseren van het MS-net ten aanzien van deze klanten worden uitgegaan van maximale belasting en minimale productie en minimale belasting en maximale productie, uiteraard in combinatie met de overige belastingen in het net.