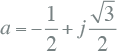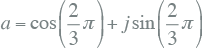Rekentechnische basis
Deel 2 begint in hoofdstuk 7 met een korte uiteenzetting van enkele belangrijke basisbegrippen die nodig zijn voor het rekenen aan elektriciteitsnetten. De basis wordt gelegd met de beschrijving van het wisselspanningsysteem en de toepassing van de complexe rekenwijze. Vervolgens wordt de voor het doen van kortsluitberekeningen zo belangrijke symmetrische componentenmethode toegelicht.
7 Rekentechnische basis
7.1 Tekenafspraken belasting en opwekking
Bij de netberekeningen wordt veel gewerkt met vervangingsschema’s voor belastingen en elektrische machines. Een elektrische machine kan zowel een motor als een generator zijn. Een motor neemt elektrische energie uit het net op en een generator levert elektrische energie. Voor de duidelijkheid wordt eerst afgesproken welke richting voor stroom, spanning en vermogen positief of negatief is. Hiervoor kan worden gekozen uit de motorconventie en de generatorconventie. Figuur 7.1 illustreert dit voor een belasting of motor en een generator die aangesloten zijn op een netwerk. Kenmerkend voor de tekenafspraak is:
- motorconventie: het aangesloten apparaat neemt actief vermogen (P, wattvermogen) uit het net op
- generatorconventie: het aangesloten apparaat levert actief vermogen (P, wattvermogen) aan het net.
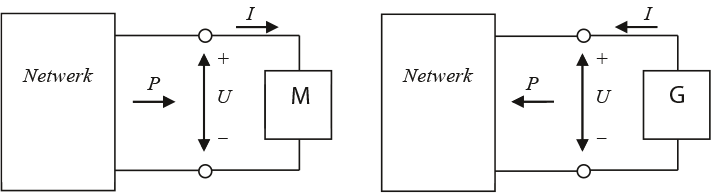
Figuur 7.1 Tekenafspraken voor motorconventie (links) en generatorconventie (rechts)
Indien het aangesloten apparaat een zuivere weerstand is, vloeit in de motorconventie de stroom van het netwerk naar het apparaat en is het teken positief. Ook het opgenomen vermogen is positief. In de generatorconventie is het teken van de stroom negatief. Het aan het netwerk afgegeven vermogen is dan ook negatief.
Spanning en stroom kunnen in het complexe vlak als wijzers worden afgebeeld. Ook de impedanties van de componenten kunnen in datzelfde vlak worden afgebeeld. De impedantie van een zuivere weerstand wordt dan gerepresenteerd met een vector op de positieve reële as. De impedantie van een zuivere spoel zonder weerstand wordt afgebeeld met een vector langs de positieve imaginaire as. De impedantie van een zuivere condensator wordt afgebeeld met een vector langs de negatieve imaginaire as. Alle fysieke componenten hebben een positieve weerstand en een positieve of negatieve reactantie. Als gevolg worden hun impedanties afgebeeld in de kwadranten I en IV in het rechtervlak van figuur 7.2. Een belasting in kwadrant I wordt inductief genoemd en een belasting in kwadrant IV capacitief.
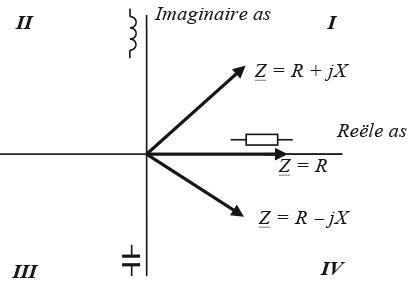
Figuur 7.2 Tekenafspraken voor de motorconventie
Een generator wordt meestal niet met een impedantie gemodelleerd. In hetzelfde vlak worden daarom ook actief vermogen en reactief vermogen (blindvermogen) afgebeeld. In het complexe vlak wordt daarbij gebruik gemaakt van de vier kwadranten. De eigenschappen voor de motor- en generatorconventie zijn samengevat in tabel 7.1.
Tabel 7.1 Tekenafspraken
Kwadrant |
Motorconventie |
Generatorconventie |
||
P |
Q |
P |
Q |
|
I |
> 0 (verbruik, motor) |
> 0 (verbruik, spoel) |
> 0 (opwekking, generator) |
> 0 (opwekking, condensator) |
II |
< 0 (opwekking, generator) |
> 0 (verbruik, spoel) |
< 0 (verbruik, motor) |
> 0 (opwekking, condensator) |
III |
< 0 (opwekking, generator) |
< 0 (opwekking, condensator) |
< 0 (verbruik, motor) |
< 0 (verbruik, spoel) |
IV |
> 0 (verbruik, motor) |
< 0 (opwekking, condensator) |
> 0 (opwekking, generator) |
< 0 (verbruik, spoel) |
Het is voor de eenduidigheid in de netberekeningen belangrijk om eenmalig te kiezen voor motor- of generatorconventie.
Ter verduidelijking van de samenhang wordt het volgende voorbeeld gegeven. Het actieve vermogen en het blindvermogen dat in de motorconventie in kwadrant III door een synchrone generator is opgewekt, wordt door een motor in kwadrant I verbruikt.
Een synchrone machine kan zowel als motor of als generator werken en kan daarbij blindvermogen opnemen en leveren. Deze machine is daarmee in staat om in alle kwadranten te werken. Maar het blijft belangrijk om ook in dit geval voor elk werkpunt eenmalig te kiezen voor hetzij de motorconventie dan wel de generatorconventie.
Ook een asynchrone machine kan zowel als motor of als generator werken maar kan daarbij alleen blindvermogen opnemen. In de motorconventie kan de asynchrone machine dan werken in de kwadranten I en II.
Tabel 7.2 Samenvatting richtingen en tekens van vermogens
Vermogen |
Motor-conventie |
Generator-conventie |
Stroom en lasthoek |
Diagram |
||
P positief |
actief vermogen opnemen |
actief vermogen leveren |
||||
P negatief |
actief vermogen leveren |
actief vermogen opnemen |
||||
Q positief |
blindvermogen opnemen (inductieve belasting) |
blindvermogen leveren (overbekrachtigde generator) |
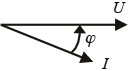
naijlende stroom hoek φ positief |
|||
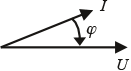
Q negatief |
blindvermogen leveren (capacitieve belasting) |
blindvermogen opnemen (onderbekrachtigde generator) |
voorijlende stroom hoek φ negatief |
7.2 Het wisselspanningsysteem
De wisselspanning kan in principe een willekeurige vorm hebben die zich elke periode herhaalt. De periode dat de vorm zich herhaalt bepaalt de frequentie f, die gelijk is aan het omgekeerde van de periodeduur. Door deze eigenschap kan de wisselspanning worden beschreven met een functie van de tijd. Het resultaat van deze functie is de momentane waarde van de spanning. In bijna alle elektriciteitssystemen is de wisselspanning sinusvormig. Het is gebruikelijk deze wisselspanning te beschrijven met onderstaande cosinusfunctie:
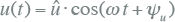 |
[ |
7.1 |
] |
waarin:
| û = √2·Ueff | topwaarde van de spanning |
| ω = 2πf | nethoekfrequentie (rad/s) |
| ψu | spanningfasehoek (rad) |
De frequentie wordt uitgedrukt in de hoekfrequentie, in radialen per seconde. De fasehoek wordt uitgedrukt in radialen, door de hoek in graden te vermenigvuldigen met 2π/360.
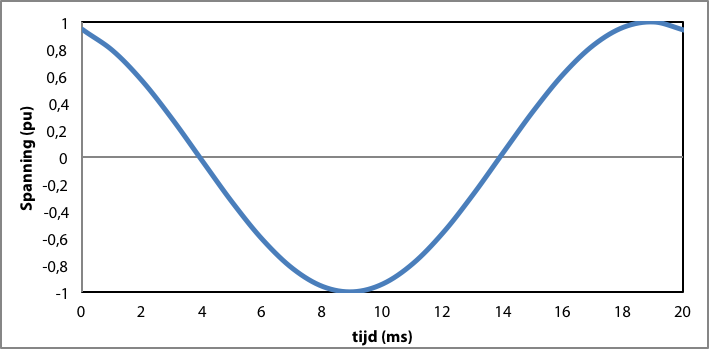
Figuur 7.3 Spanning als functie van de tijd voor f = 50 Hz en ψ = 20·(2π/360) rad
De functie van formule 7.1 beschrijft de wisselende waarde van de spanning als cosinusfunctie van de tijd. In figuur 7.3 is deze functie getekend, waarbij de fase als voorbeeld 20 graden verschoven is.
Ook de stroom is wiskundig op vergelijkbare wijze te beschrijven. De stroom heeft veelal een andere fasehoek en een andere grootte dan de spanning. Dit wordt veroorzaakt door de eigenschappen van de componenten in het netwerk en de wet van Ohm. De hoek van de stroom wordt uitgedrukt met behulp van de stroomfasehoek ψi. De momentane waarde van de stroom is dan:
 |
[ |
7.2 |
] |
waarin:
| î = √2·Ieff | topwaarde van de stroom |
| ω = 2πf | nethoekfrequentie |
| ψi | stroomfasehoek |
Het hoekverschil tussen stroom en spanning is:
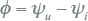 |
[ |
7.3 |
] |
Hierdoor kan de stroomfasehoek ook geschreven worden als:
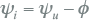 |
[ |
7.4 |
] |
waardoor vergelijking 7.2 over gaat in:
 |
[ |
7.5 |
] |
Uit de functies van de momentane waarde van stroom en spanning kan de functie voor de momentane waarde van het vermogen worden afgeleid door het product te nemen van de momentane spanning en stroom.
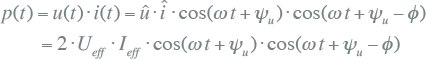 |
[ |
7.6 |
] |
Door gebruik te maken van de algemene goniometrische relaties volgt uit vergelijking 7.6:
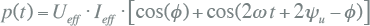 |
[ |
7.7 |
] |
Deze vergelijking kan worden opgesplitst in twee delen. Hierin valt op dat in het eerste deel de bekende cos(φ) voorkomt, die ook wel aangeduid wordt als ‘arbeidsfactor‘. Het eerste deel van de vergelijking is tijdsonafhankelijk en wordt het gemiddelde vermogen genoemd. Het tweede deel van de vergelijking is tijdsafhankelijk en wisselt met de dubbele frequentie.
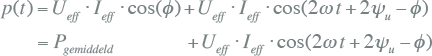 |
[ |
7.8 |
] |
Bij beschouwing van het vermogen door een zuivere weerstand is stroom zuiver resistief en is het hoekverschil tussen stroom en spanning φ = 0 rad. In dat geval vereenvoudigt formule 7.7 in:
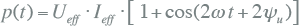 |
[ |
7.9 |
] |
Figuur 7.4 illustreert dit. Hier is duidelijk te zien dat het momentane vermogen steeds positief is en met de dubbele frequentie wisselt om het gemiddelde vermogen (P gemiddeld) van ongeveer 0,4 pu. Het gemiddelde vermogen is het vermogen waarmee arbeid wordt verricht.
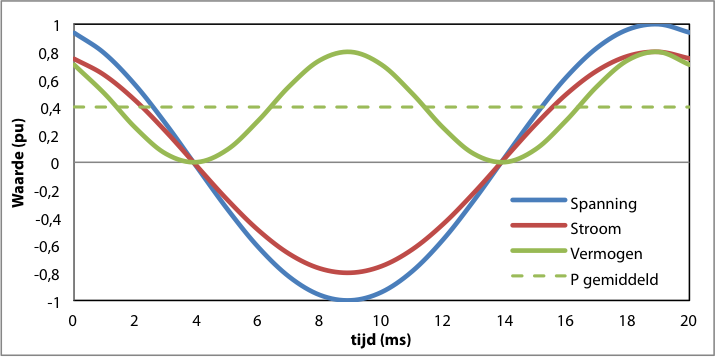
Figuur 7.4 Momentane waarden van spanning, stroom en vermogen
Het volgende voorbeeld gaat uit van een impedantie, waarbij de stroom 45 graden na-ijlt op de spanning. Volgens tabel 7.2 is dit een inductieve belasting. In geval van een 45 graden na-ijlende stroom is φ = 45·(2π/360) rad en ontstaat figuur 7.5. In deze figuur valt op dat het momentane vermogen nu niet meer altijd positief is. Het gemiddelde vermogen, waarmee arbeid wordt verricht, is in dat geval ook kleiner geworden (ongeveer 0,3 pu), doordat cos(φ) nu gelijk is aan 0,7.
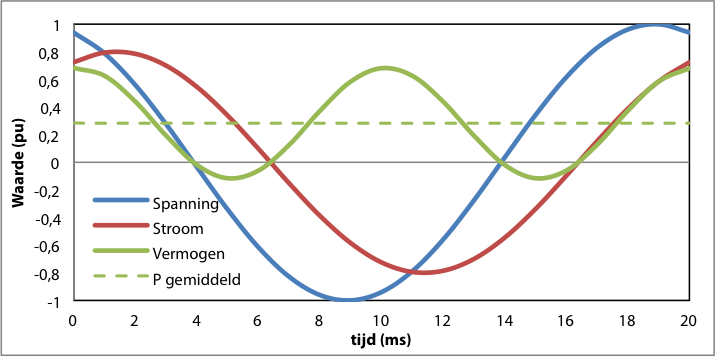
Figuur 7.5 Momentane waarden van spanning, 45 graden naijlende stroom en vermogen
In geval van een zuiver inductieve belasting ontstaat een 90 graden na-ijlende stroom met φ = 90·(2π/360) rad en ontstaat figuur 7.6. In deze figuur valt op dat het momentane vermogen even vaak positief als negatief is. Het gemiddelde vermogen, waarmee arbeid wordt verricht, is in dat geval gelijk aan nul geworden, doordat cos(φ) nu gelijk is aan 0. Dat betekent dat in dit geval geen actief vermogen wordt getransporteerd. Dat klopt, want dit is een eigenschap van een ideale spoel.
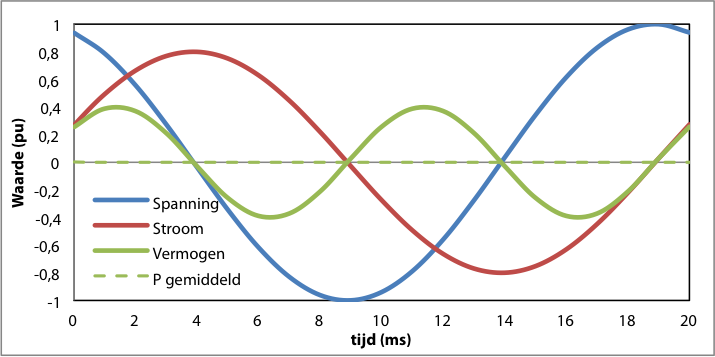
Figuur 7.6 Momentane waarden van spanning, 90 graden na-ijlende stroom (zuiver inductief) en vermogen
Het gemiddelde vermogen Pgemiddeld , waarmee arbeid wordt verricht, is gelijk aan het bekende actieve vermogen P, uitgedrukt in Watt (W).
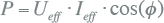 |
[ |
7.10 |
] |
Het product van de effectieve waarde van spanning en stroom wordt het schijnbare vermogen S genoemd, uitgedrukt in Volt-Ampère (VA). Dit is een zeer belangrijke waarde, omdat alle installaties op basis van het schijnbare vermogen worden ontworpen. Deze ontwerpparameter wordt op de naamplaat van onder andere transformatoren vermeld.
 |
[ |
7.11 |
] |
Hiermee kan het blindvermogen Q, het vermogensaandeel waarmee geen arbeid kan worden verricht, worden uitgerekend. Het wordt uitgedrukt in var.
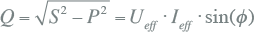 |
[ |
7.12 |
] |
7.3 Fasor-notatie in het complexe vlak
Behalve met een wisselende cosinusfunctie kan de spanning ook worden weergegeven met een ronddraaiende wijzer in het complexe vlak. De wijzer draait met dezelfde snelheid rond als de rotor van een generator, die uit twee magneetpolen is opgebouwd. De snelheid wordt uitgedrukt in de hoekfrequentie ω en is als zodanig terug te vinden in de vergelijkingen 7.1 en 7.2. Figuur 7.7 illustreert dit.

Figuur 7.7 Vergelijking ronddraaiende generatorrotor en spanningswijzer in het complexe vlak
De ronddraaiende wijzer wordt beschreven door de cosinus-tijdfunctie van vergelijking 7.1 uit te breiden met een imaginair deel, waarmee de functie van de complexe momentane waarde ontstaat. Deze uitgebreide vergelijking beschrijft de positie van de pijlpunt van de wijzer van figuur 7.7 in het complexe vlak als functie van de tijd. De functie kan worden beschreven met cosinus- en sinustermen, maar ook met een complexe e-macht.
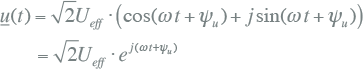 |
[ |
7.13 |
] |
De stroom wordt in het complexe vlak beschreven met onderstaande formule:
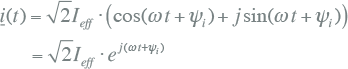 |
[ |
7.14 |
] |
Door gebruik te maken van vergelijking 7.4, kan de complexe stroomfunctie van vergelijking 7.14 ook als volgt geschreven worden:
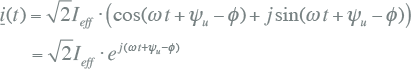 |
[ |
7.15 |
] |
De uitgebreide complexe vergelijkingen voor spanning (7.13) en stroom (7.15) zijn de basis voor het complexe rekenen met stromen, spanningen en vermogens. In de elektrische energietechniek wordt veelvuldig gebruik gemaakt van wijzers in het complexe vlak. Daarbij wordt steeds gerekend met de effectieve waarden en wordt de tijdsafhankelijkheid weggelaten. De relatie tussen de effectieve waarde en de topwaarde is een factor √2. De tijdsafhankelijkheid is in de complexe e-macht notatie vertegenwoordigd door de term ejωt. Als vergelijking 7.13 wordt gedeeld door √2 en door ejωt, gaat deze over in de tijdsonafhankelijke fasor:
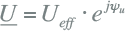 |
[ |
7.16 |
] |
Deze fasor is een wijzer in het complexe vlak, waarvan de lengte gelijk is aan de effectieve waarde Ueff van de spanning en de hoek op t=0 ten opzichte van de reële as gelijk is aan de spanningfasehoek ψu.
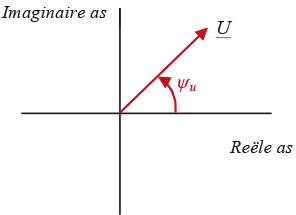
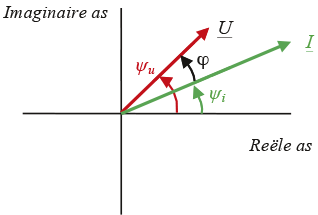
Figuur 7.8 Spanningfasor in het complexe vlak
Figuur 7.9 Spanningfasor en na-ijlende (inductieve) stroomfasor in het complexe vlak
Dit gaat ook op voor de stroom. Als evenzo vergelijking 7.15 wordt gedeeld door √2 en door ejωt, gaat deze over in de fasor-notatie voor de stroom:
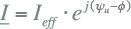 |
[ |
7.17 |
] |
Figuur 7.9 illustreert dit voor de fasors van spanning en na-ijlende (inductieve) stroom. Hierin is ook het verband tussen de fasehoeken van spanning (ψu) en stroom (ψi) en de verschilhoek (φ) zichtbaar.
Het complexe vermogen is gedefinieerd met de fasor S, waarvan de lengte S gelijk is aan het schijnbare vermogen. Het reële deel is gelijk aan het actieve vermogen P en het imaginaire deel is gelijk aan het blindvermogen Q.
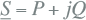 |
[ |
7.18 |
] |
Door gebruik te maken van vergelijkingen 7.10 voor P en vergelijking 7.12 voor Q gaat vergelijking 7.18 voor S over in onderstaande vergelijking, waarbij de cosinus- en sinustermen ook beschreven kunnen worden met een complexe e-macht.
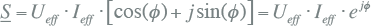 |
[ |
7.19 |
] |
De hoek van de vermogenfasor S wordt dus geheel bepaald door de hoek φ tussen de spanning- en stroomfasoren U en I. Verder uitwerken van vergelijking 7.19, door Ueff te vermenigvuldigen met ejψu en door Ieff te vermenigvuldigen met e–jψi, levert:
 |
[ |
7.20 |
] |
In vergelijking 7.20 valt het op dat de eerste term gelijk is aan de spanningfasor U en dat de tweede term, op het minteken van de complexe e-macht na, gelijk is aan de stroomfasor I. Voor het vervolg wordt nu de toegevoegd complexe waarde van de fasor I gedefinieerd, waarvoor geldt dat de imaginaire waarde een tegengesteld teken heeft:
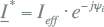 |
[ |
7.21 |
] |
Hierdoor kan het complexe vermogen als volgt worden geschreven:
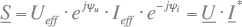 |
[ |
7.22 |
] |
Deze laatste is de bekende vergelijking waarmee het complexe vermogen direct uit de complexe spanning en stroom wordt bepaald. Deze vergelijking is de basis van elke loadflowberekening.
Bij het vergelijken van figuur 7.9 met de in tabel 7.2 gegeven vectordiagrammen wordt de relatie tussen fasehoek (voorijlend of na-ijlend) en belastingtype duidelijk. Onderstaand rekenvoorbeeld gaat hier nader op in. Uitgangspunt is een spanning van 1 V en een belasting met een inductieve impedantie van 1+j Ω. Onder gebruikmaking van de motorconventie volgt:
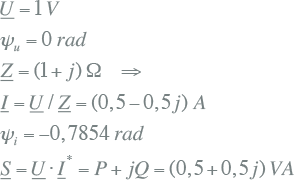 |
[ |
7.23 |
] |
Volgens vergelijking 7.23 is het actieve vermogen P gelijk aan 0,5 W en is het blindvermogen Q gelijk aan 0,5 var. Ter controle van de juistheid van de tekenafspraken van de vermogens en de fasehoeken kunnen de vermogens ook worden afgeleid uit het schijnvermogen en het hoekverschil tussen de spanning en de stroom:
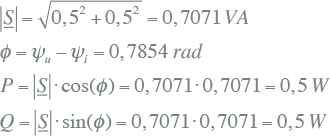 |
[ |
7.24 |
] |
7.4 Driefasen wisselstroomsysteem
De meeste wisselstroomsystemen zijn uitgevoerd als driefasensystemen, waarvan de drie fasen telkens een hoek van 120 graden met elkaar maken. In radialen is de onderlinge hoek dan gelijk aan 2/3 π. Figuur 7.10 toont hoe met drie paren van spoelen, die telkens 120 graden ten opzichte van elkaar zijn aangebracht op de stator van een generator, de spanningen worden opgewekt. In het voorbeeld zijn de spoelen in ster geschakeld. Door het linksom draaien van de rotor is de volgorde van de fasen: a, b, c.
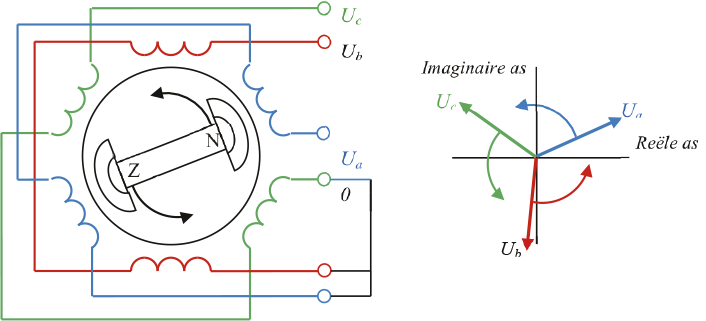
Figuur 7.10 Driefasengenerator als bron van drie fasenspanningen, in ster geschakeld
De complexe momentane spanning van een gebalanceerde driefasige spanningsbron kan, naar analogie van vergelijking 7.13 in de vorige paragraaf, worden beschreven met onderstaande drie tijdfuncties voor de fasen a, b en c. Hierin zijn de drie spanningswijzers telkens 120 graden onderling verschoven. In radialen is dat –2/3 π en –4/3 π. De waarde van –4/3 π komt overeen met +2/3 π. In de functies voor de drie spanningen wordt bij ψu voor de drie fasen respectievelijk de waarden 0, –2/3 π en +2/3 π opgeteld.
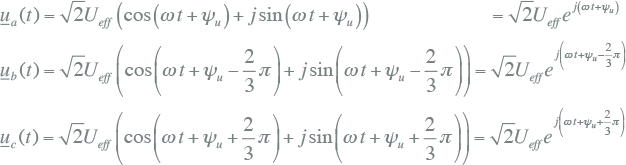 |
[ |
7.25 |
] |
In bovenstaande vergelijkingen is yu de hoek van de spanning van fase a op t=0. Figuur 7.11 illustreert dit, waarbij te zien is dat de fasevolgorde is: a-b-c. In de afbeelding is ψu gelijk aan nul genomen.
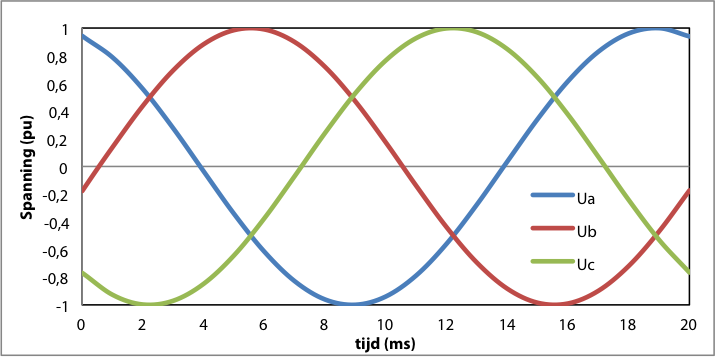
Figuur 7.11 Gebalanceerde driefasenspanningen als functie van de tijd
7.5 Methode symmetrische componenten
De berekeningen aan driefasensystemen vereisen dat gelijktijdig aan de drie fasen van het totale systeem wordt gerekend. De berekeningen worden vele malen eenvoudiger indien ervan wordt uitgegaan dat de spanningen in het system perfect driefasensymmetrisch, ofwel gebalanceerd, zijn. Een driefasensysteem wordt in dat geval gemodelleerd alsof er maar één fase aanwezig is. De spanningen in de andere fasen kunnen dan eenvoudig worden afgeleid omdat bekend is dat zij plus of min 120 graden verschillen van de berekende fase. In het vervolg wordt ervan uitgegaan dat de in het net opgestelde voedingsbronnen een gebalanceerde spanning leveren. De kabels en transformatoren worden gemodelleerd als driefasensymmetrische componenten.
Er zijn echter altijd oorzaken van onbalans, zoals een asymmetrische belasting of een asymmetrische storing in het net. Om niet terug te vallen op de berekeningen met alle fasen tegelijk, worden dit soort asymmetrische situaties in de meeste berekeningsmethoden berekend met behulp van de methode van de symmetrische componenten. Deze methode is in 1918 beschreven door Fortescue. Ook de internationale standaard IEC 60909 voor kortsluitberekeningen maakt gebruik van deze methode.
Belangrijk uitgangspunt bij de methode is dat het net symmetrisch is. De voedingen zijn over de drie fasen verdeeld en de verbindingen zijn driefasig symmetrisch. De methode van symmetrische componenten transformeert een driefasig wisselstroomnet in drie onafhankelijke enkelpolige systemen, genaamd: normaal netwerk, invers netwerk en homopolair netwerk. De Engelstalige benamingen voor deze drie systemen zijn respectievelijk: positive sequence, negative sequence en zero sequence. De specifieke onbalans op een foutplaats bepaalt de wijze waarop de drie onafhankelijke enkelpolige systemen (componentennetwerken) met elkaar worden verbonden. Een belangrijk voordeel van deze methode is dat netten en storingen in netten met deze methode eenvoudig kunnen worden doorgerekend. De methode maakt het mogelijk de berekeningen met de hand uit te voeren.
7.5.1 Een nieuwe fasor-notatie
De basis voor de symmetrische componentenmethode wordt gevormd door drie vectoren in het complexe vlak, die 120 graden van elkaar zijn verschoven en de lengte 1 hebben. De methode introduceert een complexe vector a, van lengte 1 en met een hoek van 120 graden ten opzichte van de reële as. Een hoek van 120 graden is gelijk aan 2/3 π radialen. Deze vector kan op diverse manieren worden beschreven:
|
[ |
7.26 |
] |
Door een vector met a te vermenigvuldigen ontstaat een nieuwe vector die 120 graden, ofwel 2/3 π, verder gedraaid is. Zo ontstaat de vector a2 door de vector a met zichzelf te vermenigvuldigen. De hoek is 240 graden, ofwel 4/3 π, ten opzichte van de reële as en dat is gelijk aan –120 graden, ofwel –2/3 π. Figuur 7.12 illustreert dit voor de vectoren 1, a en a2.
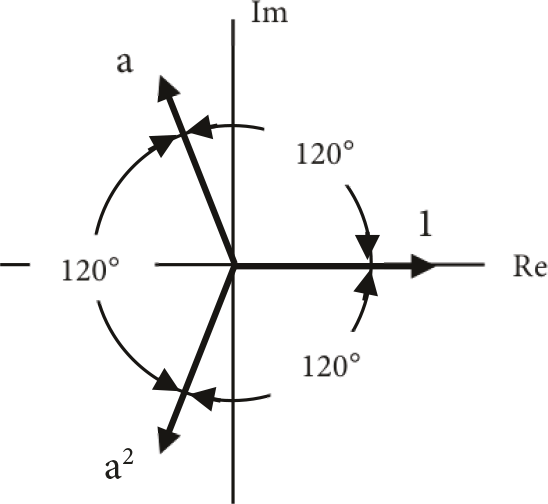
Figuur 7.12 Vectoren 1, a en a2 in het complexe vlak
De drie vectoren worden op de volgende wijze als complexe e-macht of polair beschreven:
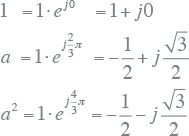 |
[ |
7.27 |
] |
De vectoriële som van deze drie vectoren is gelijk aan nul. Dat betekent dat:
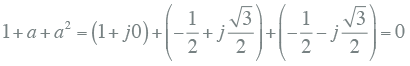 |
[ |
7.28 |
] |
Met behulp van deze vectoren kunnen de vergelijkingen van vergelijking 7.25 voor de momentane waarden van de spanning van een gebalanceerd stelsel ook als volgt geschreven worden:
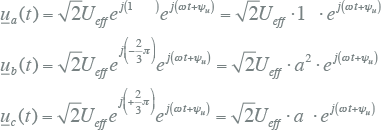 |
[ |
7.29 |
] |
Hierbij wordt opgemerkt dat e -j 2/3 π gelijk is aan e j 4/3 π. Uit vergelijking 7.29 kan geconcludeerd worden dat een gebalanceerd stelsel spanningsvectoren kan worden beschreven met één linksom roterende vector, vermenigvuldigd met drie vectoren die elk 120 graden ten opzichte van elkaar zijn verschoven.
In de complexe fasor-notatie gaat het stelsel vergelijkingen van 7.29 voor een driefasensymmetrisch spanningsstelsel op dezelfde manier als vergelijking 7.16, door te delen door √2 en door ejωt, over in:
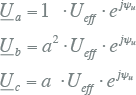 |
[ |
7.30 |
] |
7.5.2 Splitsing in drie spanningsstelsels
Het idee van Fortescue was om ieder willekeurig ongebalanceerd stelsel van vectoren te beschrijven met behulp van drie onafhankelijke gebalanceerde linksom draaiende stelsels van vectoren, genaamd het normale, inverse en homopolaire stelsel. In het homopolaire stelsel zijn de drie vectoren gelijk aan elkaar en gelijk gericht. In het normale stelsel zijn de drie vectoren gelijk aan elkaar en maken zij een hoek van 120 graden ten opzichte van elkaar. In het normale stelsel is de vectorvolgorde a-b-c.
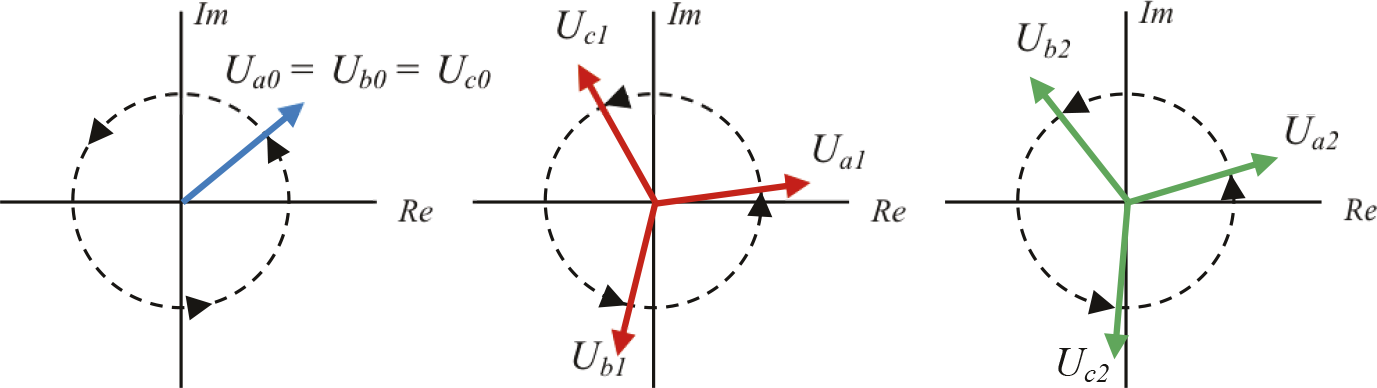
Figuur 7.13 Spanningen in het homopolaire, normale en inverse stelsel
Ook in het inverse stelsel zijn de drie vectoren gelijk aan elkaar en maken zij een hoek van 120 graden ten opzichte van elkaar, maar is de vectorvolgorde a-c-b. Elk componentstelsel heeft een eigen specifieke hoekverdraaiing ten opzichte van de reële as. Deze drie componentstelsels zijn hierboven afgebeeld. Met de drie vectorstelsels van figuur 7.13 kunnen alle (asymmetrische) driefasenstelsels worden samengesteld. Dit wordt geïllustreerd aan de hand van een voorbeeld. Onderstaand voorbeeld geeft de constructie weer van een willekeurig asymmetrisch spanningsstelsel.
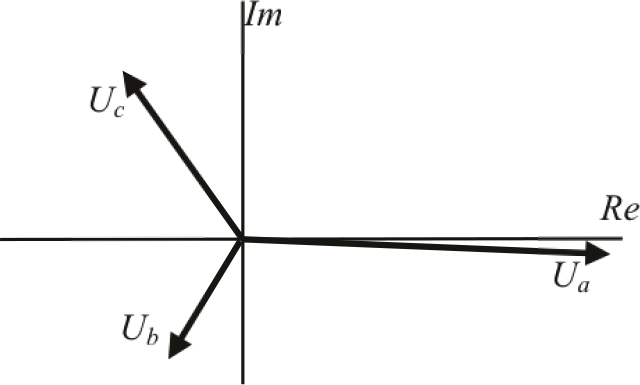
Figuur 7.14 Voorbeeld van een asymmetrisch spanningsstelsel
Hieronder zal met behulp van een grafische decompositie worden aangetoond dat dit stelsel kan worden samengesteld met behulp van:
- homopolaire component: 20% en hoek 10°
- normale component: 100% en hoek 0°
- inverse component: 30% en hoek –20°
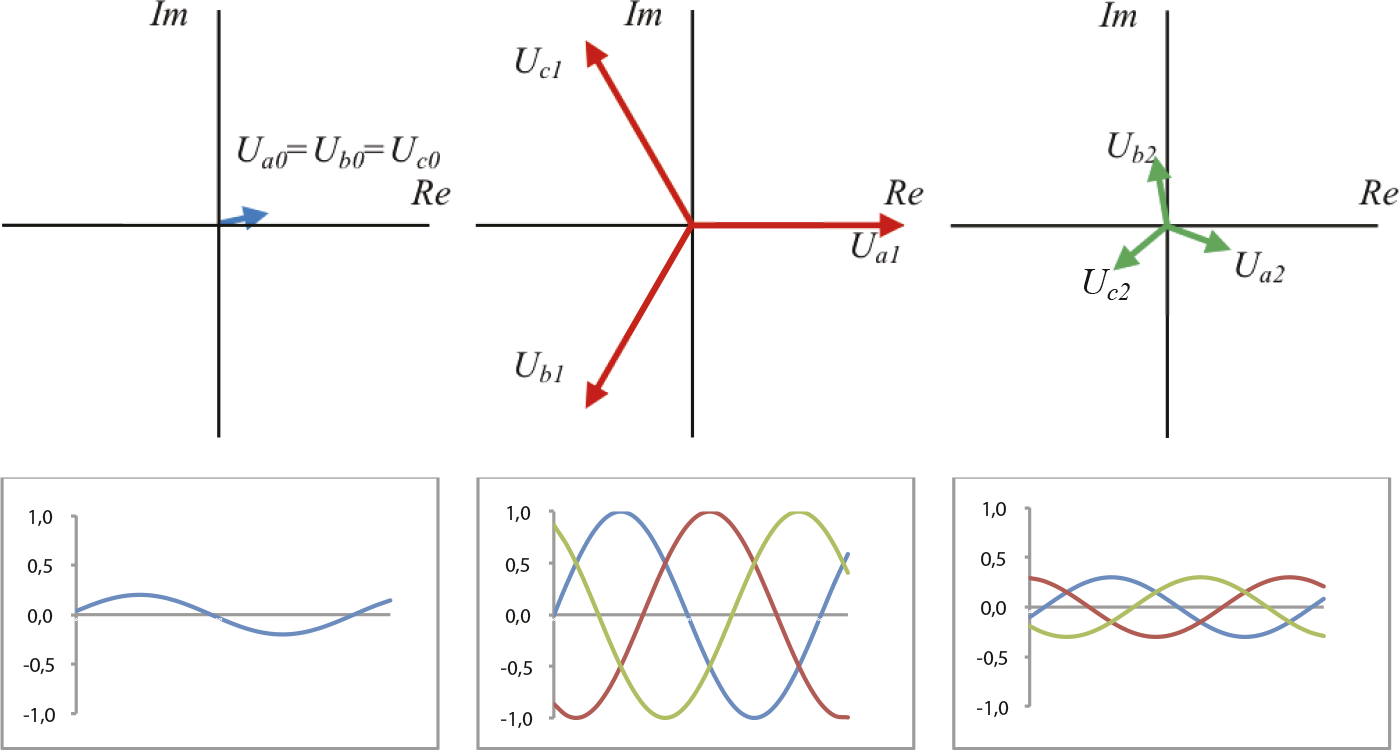
Figuur 7.15 Spanningen in het homopolaire, normale en inverse stelsel
Het asymmetrische stelsel wordt geconstrueerd door voor elke fase de vectoren op te tellen. Zo geldt voor de drie fasen:
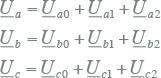 |
[ |
7.31 |
] |
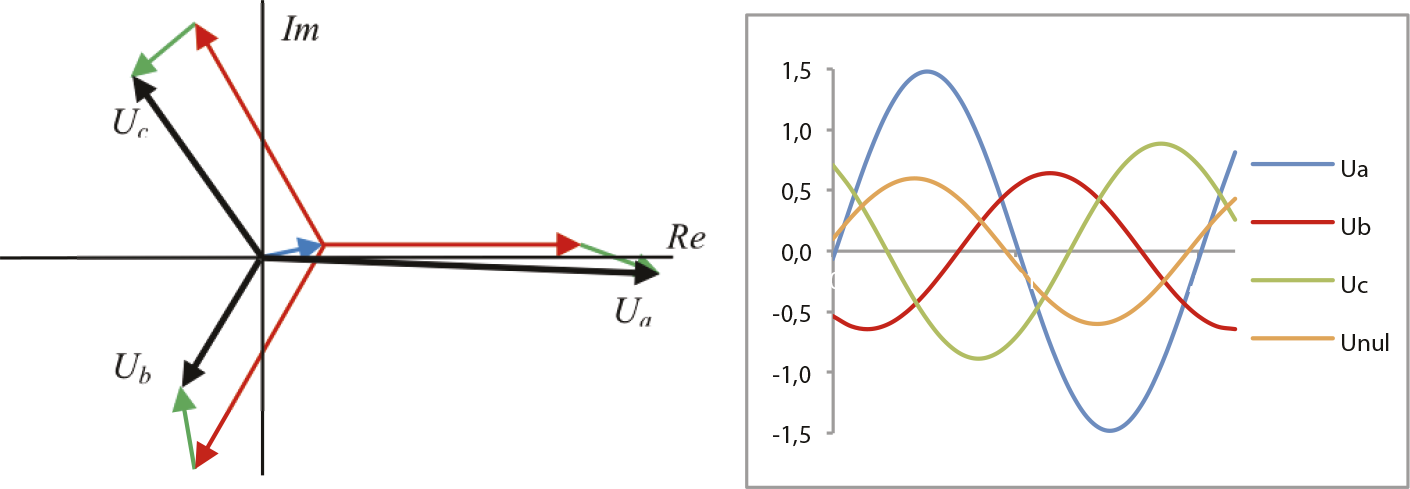
Figuur 7.16 Constructie van een asymmetrisch stelsel uit het homopolaire, normale en inverse stelsel
7.5.3 Wiskundige decompositie
De componentspanningen van figuur 7.15 kunnen worden ontbonden in drie genormeerde componentstelsels, die zijn opgebouwd met de vectoren 1, a en a2, en drie bijbehorende complexe vectoren. Figuur 7.17 geeft de ontbinding van de drie componentstelsels van figuur 7.15 weer.
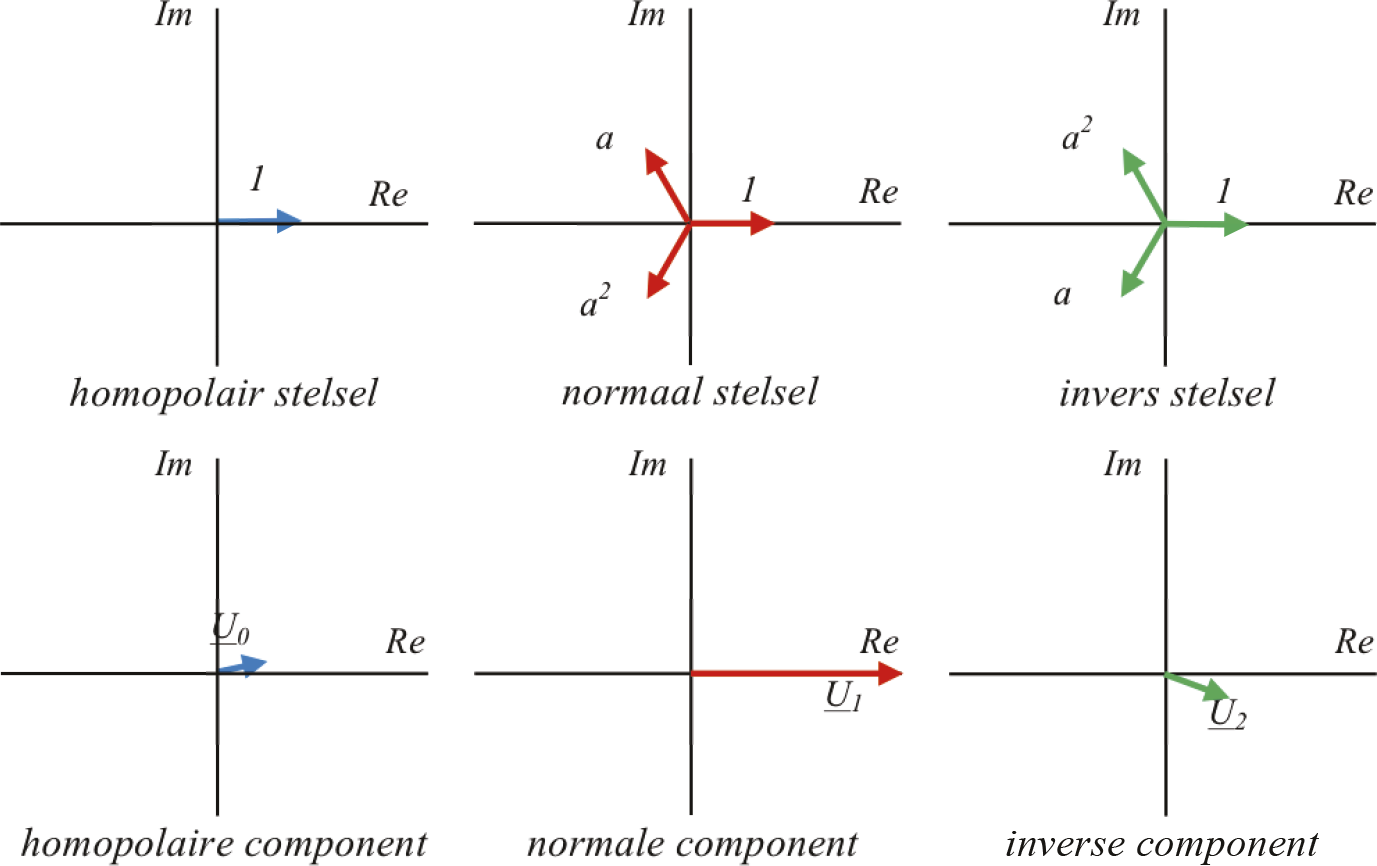
Figuur 7.17 Genormeerde homopolaire, normale en inverse stelsels met vermenigvuldigingsfactoren
Voor het stelsel van figuur 7.15 kunnen alle vectoren worden beschreven met behulp van de drie genormeerde componentenstelsels en hun complexe vermenigvuldigingsfactoren. In de vergelijkingen 7.32 zijn de vermenigvuldigingsfactoren U0, U1 en U2 de complexe spanningsvectoren die voor ieder componentstelsel de effectieve waarde en de fasehoek vastleggen. Bijvoorbeeld voor fase b geldt:
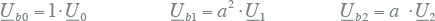 |
[ |
7.32 |
] |
Analoog aan vergelijking 7.31 kan de constructie van elk driefasensystelsel vanuit de genormeerde symmetrische componenten worden beschreven als de som van de drie componentspanningen:
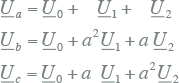 |
[ |
7.33 |
] |
Dit kan worden omgezet in een matrixvergelijking. Het stelsel van vergelijking 7.33 gaat dan over in vergelijking 7.34, waarbij de matrix A de transformatiematrix wordt genoemd.
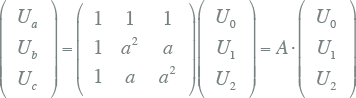 |
[ |
7.34 |
] |
Van het voorbeeld van figuur 7.14 zijn de complexe waarden van de drie componenten:
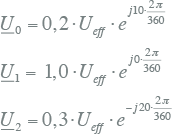 |
[ |
7.35 |
] |
Door deze waarden in te vullen in de vergelijkingen 7.33, worden de waarden van de fasen van het asymmetrische spanningsstelsel berekend:
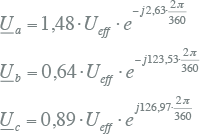 |
[ |
7.36 |
] |
De fysische analogie kan het best worden aangetoond met figuur 7.18, waar een asymmetrische spanningsbron wordt beschreven met een serieschakeling van de
drie componentspanningsbronnen. Het is echter een fictieve ontbinding, aangezien de homopolaire, inverse en normale spanningsbronnen in werkelijkheid niet
bestaan.
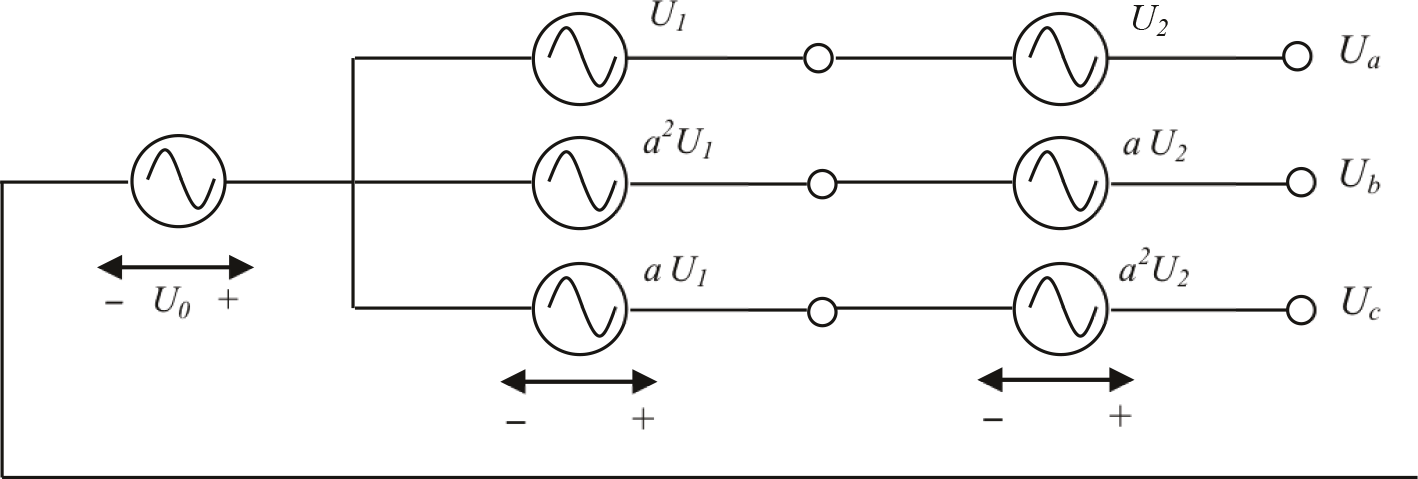
Figuur 7.18 Fysische interpretatie van het samenstellen met componentensystemen
In het ideale gebalanceerde geval is U0 = 0 en U2 = 0 zodat we alleen te maken hebben met U1. In praktijk is echter U0 ≠ 0 en U2 ≠ 0. Dit wordt veroorzaakt door de onbalans in het driefasensysteem.
Het is dus mogelijk om de fysieke spanningen Ua, Ub en Uc in een driefasenstelsel te beschrijven met behulp van de componentspanningen U0, U1 en U2. Omgekeerd is het ook mogelijk om de componentspanningen te berekenen uit de fysieke spanningen. Door het stelsel vergelijkingen van 7.33 te inverteren, worden de navolgende vergelijkingen voor de decompositie uit de fysieke grootheden verkregen.
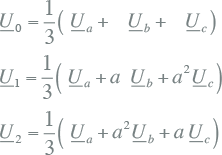 |
[ |
7.37 |
] |
Ook dit kan worden opgeschreven als een matrixvergelijking. Hierbij is de matrix A-1 de inverse transformatiematrix. Hiermee worden de grootheden van het componentensysteem afgeleid uit de grootheden van het fysieke systeem, zodat de componentspanningen in matrixnotatie als volgt worden berekend:
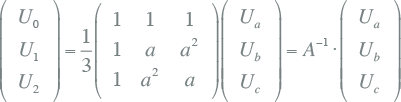 |
[ |
7.38 |
] |
Samengevat geldt voor de transformatiematrix en de inverse transformatiematrix:
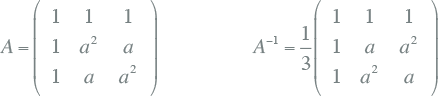 |
[ |
7.39 |
] |
De toestand in het net wordt niet alleen met spanningen beschreven maar ook met stromen. Voor de stroomvectoren Iabc en I012 kunnen de hierboven beschreven transformaties op dezelfde manier worden uitgevoerd. In matrixnotatie ziet dat er als volgt uit:
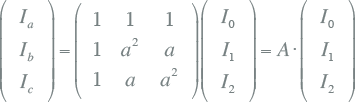 |
[ |
7.40 |
] |
Het kan worden aangetoond dat ook impedanties van driefasensystemen beschreven kunnen worden met behulp van de symmetrische componentenmethode. Met de wet van Ohm en het gebruiken van de transformatie voor de stroom- en spanningsvectoren volgt namelijk:
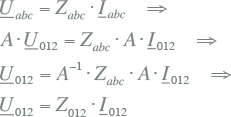 |
[ |
7.41 |
] |
Hierin zijn Uabc , Iabc en Zabc respectievelijk de spanningsmatrix, de stroommatrix en de impedantiematrix in het abc-stelsel en zijn U012 , I012 en Z012 respectievelijk de spanningsmatrix, de stroommatrix en de impedantiematrix in het componentenstelsel. Voor de relatie tussen de impedantiematrix in het abc- en componentenstelsel geldt:
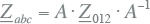 |
[ |
7.42 |
] |
Ook elke kabelverbinding, transformator, belasting en opwekker kan worden gemodelleerd met normale, inverse en homopolaire impedanties. Voor de meeste berekeningen is het voldoende als wordt aangenomen dat de systemen driefasensymmetrisch zijn. In dat geval vereenvoudigt het systeem zodanig dat alleen rekening hoeft worden gehouden met de normale impedantie Z1 en de homopolaire impedantie Z0. De normale impedantie is gelijk aan de fase-impedantie. De inverse impedantie hoeft niet apart te worden bepaald, want deze is in dit geval gelijk aan de normale impedantie. De homopolaire impedantie wijkt af van de normale impedantie en moet wel apart vastgesteld worden. De volgende paragraaf beschrijft een asymmetrisch stroomstelsel en de homopolaire impedantie.
7.6 Asymmetrisch stroomstelsel en homopolaire impedantie
Figuur 7.19 is een uitbreiding op figuur 7.18, waarin een spanningsbron met homopolaire, normale en inverse componenten (U0, U1 en U2) zijn opgenomen. Achter de samengestelde spanningsbron is een willekeurig driefasencircuit met een retourpad opgenomen. Het driefasencircuit bestaat uit de impedanties Za, Zb en Zc , die niet gelijk aan elkaar hoeven te zijn. In de meeste driefasensystemen zijn deze drie impedanties wel gelijk aan elkaar, waardoor aangenomen mag worden dat de normale impedantie Z1 gelijk is aan de fase-impedantie, bijvoorbeeld Za. De inverse impedantie Z2 is dan gelijk aan de normale impedantie. Er is een retourpad met een retourimpedantie ZE. Het retourpad kan een vierde geleider zijn, zoals bij LS-kabels, en het kan door aarde lopen, zoals in MS-netten.
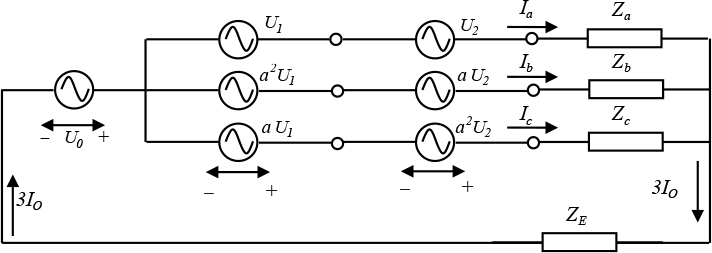
Figuur 7.19 Voedingsbron met belasting en retourimpedantie
De van vergelijkingen 7.40 afgeleide componenttransformatie beschrijft de relatie tussen de stromen in het fictieve componentnetwerk en het fysieke stelsel:
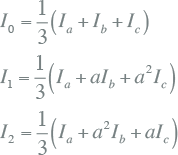 |
[ |
7.43 |
] |
Hieruit blijkt dat de homopolaire stroom gelijk is aan een derde van de som van de drie fasestromen. In geval van een perfect gebalanceerd driefasensysteem, zal de homopolaire stroom nul zijn. In geval van een niet gebalanceerd systeem loopt er een retourstroom en is uit figuur 7.19 af te leiden dat deze gelijk is aan de vectoriële som van de drie fasenstromen en dus gelijk is aan: IE = Ia + Ib + I c = 3I0.
Hieruit kan een manier worden afgeleid om de homopolaire impedantie te meten. Dit vindt plaats door het aanbrengen van een homopolaire spanning op de drie parallelgeschakelde fasen, zoals aangegeven in figuur 7.20. De amplitudes van de normale en inverse spanningsbronnen (U1 en U2) zijn in dat geval nul.
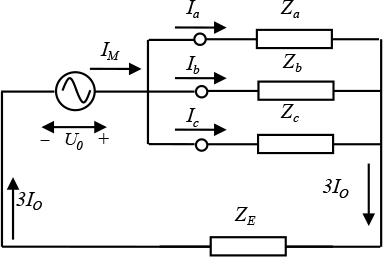
Figuur 7.20 Meting van de homopolaire impedantie
In een gebalanceerd driefasensymmetrisch net geldt voor de te meten lijnimpedantie: ZL = Za = Zb = Zc , zodat voor de stromen geldt: Ia = Ib = Ic = I0. Dan is uit de afbeelding af te leiden dat voor de meting volgt:
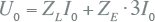 |
[ |
7.44 |
] |
Uit bovenstaande vergelijking volgt voor de homopolaire impedantie:
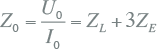 |
[ |
7.45 |
] |
Tijdens de meting worden drie fasen kortgesloten en wordt derhalve de parallelschakeling van drie homopolaire impedanties gemeten: IM = 3I0. Als gevolg wordt de homopolaire impedantie uit de meting bepaald door de gemeten impedantie met 3 te vermenigvuldigen.
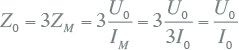 |
[ |
7.46 |
] |
De homopolaire impedantie wordt dus bepaald door het totale retourcircuit, dat bestaat uit de nulgeleider (indien aanwezig), de afscherming en wapening van de kabel, de grond, geleidende buizen, tram- en treinrails en alle andere geleidende voorwerpen in het retourcircuit. Dit maakt het zo moeilijk de waarde van de homopolaire impedantie te berekenen. Om die reden is het verstandig van belangrijke circuits, voordat zij in bedrijf worden genomen, de homopolaire impedantie te meten.
7.7 Rekenen met behulp van genormeerde grootheden
In veel berekeningsprogramma’s wordt niet gerekend met de werkelijke fysische grootheden, maar met genormeerde grootheden. Dit wordt gedaan zodat het mogelijk wordt om tegelijkertijd aan laagspannings- middenspannings en hoogspanningssystemen te rekenen, waarvan de grootheden numeriek onderling veel verschillen. In computerprogramma’s zou gebruik van fysische grootheden namelijk kunnen leiden tot numerieke problemen. De genormeerde grootheden worden uitgedrukt in per unit (pu). Een tweede voordeel van deze methode is dat het met de hand berekenen van kortsluitstromen over de spanningniveaus van meerdere transformatoren veel eenvoudiger wordt.
Alle grootheden worden genormeerd met behulp van basisgrootheden. Een aantal basisgrootheden wordt gekozen, waarna de overige basisgrootheden worden afgeleid. Meestal wordt de basisgrootheid voor spanning en voor vermogen gekozen, waarna de basisgrootheden voor stroom en impedantie worden afgeleid. Indien de basisgrootheid van het vermogen willekeurig gekozen wordt en de basisgrootheid van de spanning gelijk genomen wordt aan de nominale spanning per spanningniveau, geldt voor de basisgrootheden:
| Sbasis | keuze voor een 3-fasig basis vermogen | (MVA) |
| Ubasis | gekoppelde spanning per spanningsniveau | (kV) |
| Ibasis | basis fasestroom: 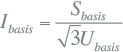 |
(kA) |
| Zbasis | basis impedantie: 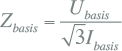 |
(Ω) |
Indien in de relatie voor de basisimpedantie teller en noemer met Ubasis vermenigvuldigd worden, gaat deze over in:
| Zbasis | basis impedantie: 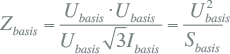 |
(Ω) |
De relatie tussen vermogen, spanning, stroom en impedantie is aldus bepaald:
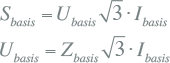 |
[ |
7.47 |
] |
De genormeerde grootheden worden dan als volgt afgeleid uit de fysische grootheden en hun basisgrootheden:
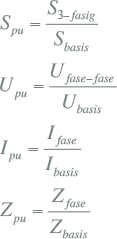 |
[ |
7.48 |
] |
Als gevolg geldt voor de wet van Ohm:
 |
[ |
7.49 |
] |
Door links en rechts van het gelijkteken te delen door de basisspanning, volgens de bovenstaande definitie, volgt dezelfde uitdrukking in per unit:
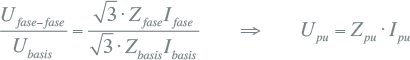 |
[ |
7.50 |
] |
Bij het gebruik van het per unit systeem geldt voor de per unit-waarden:
- het vermogen representeert het driefasig vermogen
- de spanning representeert de gekoppelde spanning
- de stroom representeert de fasestroom
- de impedantie representeert de fase-impedantie.