The result of the calculation is the eigenvalues of the A-matrix of the linearized network model. If all eigenvalues are located on the left half-part of the complex plane (with respect to the imaginary axis), then the system is stable. The more to the left the eigenvalues are, the more stable the system is. Imaginary part of an eigenvalue is related with the frequency of oscillation of respective mode.
After performing the computation the following window appears:
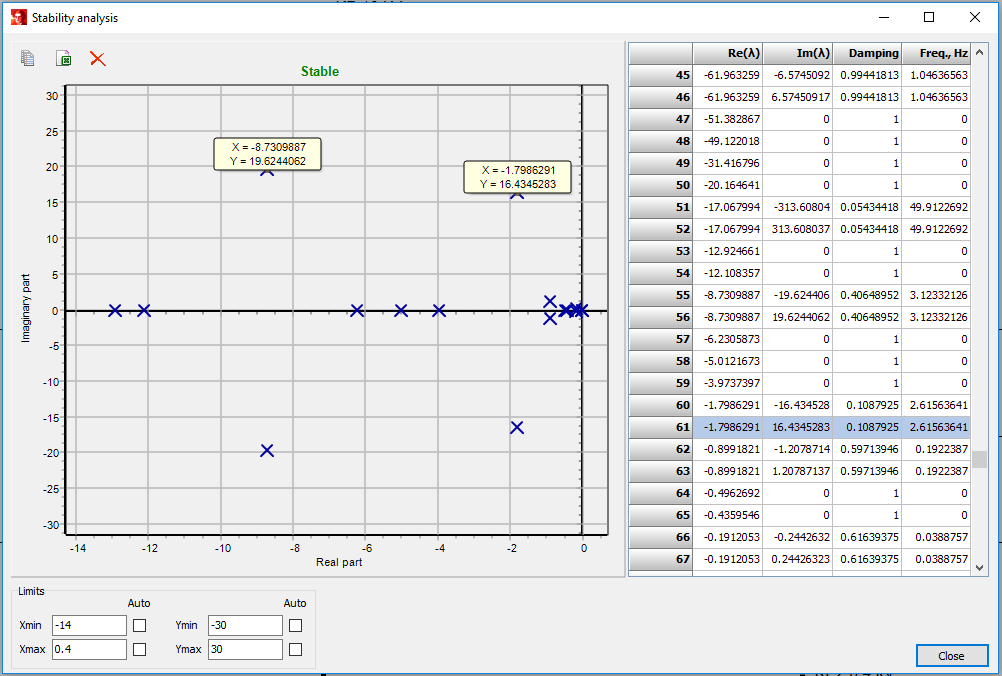
The eigenvalues are shown graphically on the plot. The limits of the plot can be set automatically or adjusted manually. If an eigenvalue in the plot area is clicked, the respective value is selected in the table. A double click on an eigenvalue in the plot area gives a label with values of real and imaginary parts of this eigenvalue on the figure. The labels can be deleted using button Delete marks (see the upper-left part of the plot). Next to it the button Copy plot to the clipboard is located, which can be used to copy the plot graphically and paste it, for instance, to Microsoft Word. The button Export to Excel exports detailed information of stability analysis results. The following information is exported:
•A-matrix of the linearized network model;
•description of the states;
•eigenvalues, respective damping and oscillation frequency;
•right and left eigenvectors;
•participation factors.
Participation factors (visible only in the exported Excel file) contain important information about the behavior of the system. They give indication of which state influences which eigenvalue the most. Participation factors in Vision are normalized and given in per cent such that the sum of all participation factors per column has to be 100%. However, small participation factors (less than 0.01%) are neglected in order to keep the overview more readable. Therefore, small deviations from 100% can be present.
Participation factors can be analyzed in the following manner. First, the eigenvalues can be checked. The number of the eigenvalue with the worst damping (that has its real part the closest to zero) can be noted. The column with the noted number can be located on tab Participation factors. Then the state number for the largest participation factor in the column can be determined. Using this state number it can be traced on tab States – which component and which variable cause the bad damping.