<< Click to Display Table of Contents >> Navigation:  Componenten en parameters > Takken > Driewikkelingstransformator

De driewikkelingstransformator is een object die vele uitvoeringsvormen kent. Zo zijn door de combinaties van schakelingen van de wikkelingen vele gangbare en minder gangbare typen denkbaar. Dit hoofdstuk gaat in op de invoervelden. Voor meer achtergrondinformatie, zie: http://www.phasetophase.nl/pdf/driewikkeltransformator.pdf.

 

 

PARAMETERS

 

Algemeen

De wikkelingen van de driewikkelingstransformator worden door Vision automatisch aan de knooppunten in het net toegewezen. De primaire wikkeling wordt altijd aan het knooppunt met de hoogste nominale spanning toegewezen. De tertiaire wikkeling wordt altijd aan het knooppunt met de laagste nominale spanning toegewezen. In het geval dat knooppunten gelijke nominale spanningen hebben, worden de wikkelingen toegewezen in volgorde van invoer van de knooppunten door de gebruiker. Dus als ingevoerd wordt: 380 / 50 / 380 kV en de knooppunten deze volgorde hebben, zijn de primaire en secundaire wikkelingen 380 kV en is de tertiaire wikkeling 50 kV.

 

 

Driewikkelingstransformator

 

 

1)   De defaultwaarde van de nominale spanning wordt gelijk gekozen aan de nominale spanning van het knooppunt waar de wikkeling op is aangesloten

2)   De defaultschakeling en klokgetal worden gekozen aan de hand van de nominale spanning van de betreffende wikkeling

 

Unom

Bij een nieuwe driewikkelingstransformator wordt voor Unom,w1, Unom,w2 en Unom,w3 de nominale spanning van de betreffende knooppunten overgenomen.

 

Type

In de typelijst bevinden zich alle transformatoren uit het typenbestand waarbij Unom,w1, Unom,w2 en Unom,w3 tussen 0.8*Unom en 1.2*Unom van de drie knooppunten liggen.

Zie ook: Type

 

Klokgetal

Het klokgetal is van belang om bij asymmetrische sluitingen de fasespanningen en fasestromen "voorbij" de transformator te kunnen berekenen.

 

bij S

Voor het berekenen van de transformatorparameters uit uk en Pk wordt standaard gebruik gemaakt van het minimum van de nominale vermogens van de twee betrokken wikkelingen. Indien bij S voor de betreffende parameters is ingevuld wordt deze waarde gebruikt in plaats van de standaardwaarde.

 

Trapschakelaar

De aanduiding van de trapstand kan volledig door de gebruiker worden gedefinieerd door de minimale, nominale en maximale trapstand aan te geven. Let op dat bijvoorbeeld de minimale trapstand kan zijn gedefinieerd als de trapstand bij het kleinst aantal windingen en daarmee (afhankelijk van de trapzijde) de grootste overzetverhouding kan geven!

 

Z0 en R0

Uitgangspunt voor de invoer van de homopolaire impedanties is altijd een meting. De meetwaarden zijn terug te vinden in het meetrapport. Afhankelijk van het type schakeling zijn de homopolaire impedanties meetbaar en van toepassing. Soms volstaat een enkele meting (bijvoorbeeld bij een YNdd-transformator) maar soms zijn drie metingen nodig. Bij de metingen moeten dan soms wikkelingen worden kortgesloten (YN-wikkelingen). Indien een wikkeling voor de meting wordt kortgesloten, kan het zijn dat de waarde van twee parallelgeschakelde wikkelingen (bijvoorbeeld een kortgesloten YN- en een D-wikkeling) gemeten wordt.

Bij 98 van alle 125 mogelijke schakelingen moeten de homopolaire impedantie (Z0) en weerstand (R0) worden ingevuld volgens onderstaande tabel. Dit geldt ook voor de waarden in het typenbestand. Een meting kan alleen vanaf een YN-wikkeling of vanaf een ZN-wikkeling worden uitgevoerd. Een ZN-wikkeling heeft overigens geen doorgaande homopolaire koppeling met andere wikkelingen. Voor elke transformatorconstructie is in de onderstaande tabel met behulp van een code aangegeven of er ten behoeve van de metingen wikkelingen kortgesloten zijn. Indien voor een meting een YN-wikkeling aan een andere zijde kortgesloten is, wordt dit aangeduid met een uitroepteken (bijvoorbeeld: meten aan wikkeling 1 met wikkeling 2 kortgesloten: w1 -> w2! ). Een D-wikkeling is per definitie altijd kortgesloten voor homopolaire stromen en dit wordt niet expliciet in de code aangegeven. Een meting vanaf een wikkeling kan ook worden uitgevoerd met de beide andere twee wikkelingen kortgesloten (kortgesloten YN of D). In het netwerkmodel staan deze twee wikkelingen voor de homopolaire stromen parallel. Dit wordt in de tabel aangegeven met // (bijvoorbeeld: meten aan wikkeling 1 met wikkeling 2 een kortgesloten YN-wikkeling en wikkeling 3 een D-wikkeling: w1 -> w2! // w3 ).

 

Indien, bijvoorbeeld, een YNYND-transformator wordt bemeten, zijn er vier verschillende manieren om de homopolaire impedanties te meten:

1.meet wikkeling 1, met wikkeling 2 open; in dat geval wordt wikkeling 1 en de transformatie van wikkeling 3 (driehoekwikkeling) gemeten (aangeduid met: w1->w3).

2.meet wikkeling 1, met wikkeling 2 kortgesloten; in dat geval wordt wikkeling 1 en de transformatie van wikkeling 2 (kortgesloten YN) parallel met wikkeling 3 (driehoekwikkeling) gemeten (aangeduid met: w1->w2!//w3).

3.meet wikkeling 2, met wikkeling 1 open; in dat geval wordt wikkeling 2 en de transformatie van wikkeling 3 (driehoekwikkeling) gemeten (aangeduid met: w2->w3).

4.meet wikkeling 2, met wikkeling 1 kortgesloten; in dat geval wordt wikkeling 2 en de transformatie van wikkeling 1 (kortgesloten YN) parallel met wikkeling 3 (driehoekwikkeling) gemeten (aangeduid met: w2->w1!//w3).

 

Er zijn maar drie van de vier metingen nodig om de homopolaire netmodelparameters af te leiden. In bovenstaand voorbeeld zijn voor de YNYND-transformator de metingen 1, 2 en 3 geïmplementeerd in onderstaande tabel.

 

In onderstaande tabel zijn alle metingen opgesomd die worden gebruikt voor het afleiden van de modelparameters. De aangegeven meetresultaten worden ingevoerd in het transformatorform voor de homopolaire impedanties.

 

 

Homopolaire impedantie bij YNyy- en YNyz-driewikkelingstransformator

Bij een transformator, bestaande uit één geaarde sterwikkeling en twee niet geaarde wikkelingen in ster of zigzag, wordt de homopolaire impedantie van de geaarde wikkeling niet verwaarloosd. Als gevolg moet in netten waar deze transformatoren zijn gemodelleerd, voor de homopolaire impedantie van de geaarde sterwikkeling een waarde groter dan nul worden ingevuld. Default is de waarde weliswaar altijd nul, maar de waarde voor de homopolaire impedantie van een transformator is een factor maal de normale impedantie. De factor is afhankelijk van de bouw van de kern van de transformator. Zie onderstaande tabel.

 

 

Aansluiting

 

 

Snom'

De term Snom' is geïntroduceerd voor het signaleren van een overbelasting in de loadflow. Deze waarde is geïntroduceerd om eenduidigheid te krijgen over de maximale belastbaarheid van een tak. Snom1', Snom2' en Snom3' worden overgenomen uit de typegegevens of uit de opgegeven waarde.

 

Spanningsregeling

 

 

1)   De defaultwaarde wordt gelijk gekozen aan de nominale spanning van de transformatorwikkeling die zich aan de meetzijde bevindt

 

Bij het gebruik van de meester-slaaf-regeling met parallelle transformatoren, wordt door de slaven de overzetverhouding van de meester gekozen of benaderd bij ongelijke typen.

 

Stroomcompensatie

Bij loadflowberekeningen kan Vision met behulp van de spanningsregeling een juiste trapstand bepalen, waarbij rekening wordt gehouden met de secundaire stroom (Ij) en een compounderingsimpedantie Zc. De trapstand wordt zodanig bepaald dat de spanning aan de meetzijde (w1 of w2) binnen de aangegeven spanningsgrenzen Umin en Umax, gecorrigeerd met het product van Ij en Zc, zal liggen. In onderstaande figuur is een voorbeeld van transformator met spanningsregeling weergegeven met trapzijde w1 (i), meetzijde w2 (j) en een fictief meetpunt aan de w2-zijde (let op de richting van Ij ).

 

 

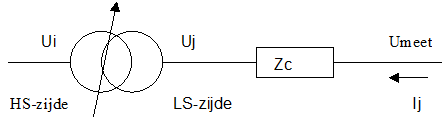
De spanning Umeet, op basis waarvan de spanningsregeling een andere trapstand kiest, is:

 Umeet = Uj + Ij * Zc

waarin:

 Zc = Rc + jXc

 

De compoundering in Vision houdt door de complexe vermenigvuldiging rekening met de richting van de stroom. Let op: in de praktijk kan het voorkomen dat wordt uitgegaan van de absolute stroomwaarde. In die gevallen zal het model van de spanningsregeling bij teruglevering anders reageren dan in de praktijk.

 

Als Umeet > Umax of Umeet < Umin aan w2-zijde dan wordt aan w1-zijde een andere trapstand gekozen (tot de minimale of maximale trapstand is bereikt).

Als de U-regeling het spanningsverlies over een bepaalde verbinding moet compenseren, kan dit door het aangeven van een compounderingsimpedantie Zc. Op welke wijze Zc kan worden bepaald uit een grafiek U = f(I), is aangegeven aan de hand van de volgende figuur.

 

Als Rc/Zc = cosbelasting dan geldt:

 U / I = Zc

waarmee Rc en Xc kan worden bepaald:

 Rc = Zc * cos(phi)belasting

 Xc = Zc * sin(phi)belasting

 

Worden de gevonden waarden voor Rc en Xc in het formulier opgegeven, dan zal de transformatorspanning afhankelijk zijn van de belastingsstroom.

Voor meer informatie, zie: http://www.phasetophase.nl/pdf/stroomcompensatie.pdf

 

Betrouwbaarheid

 

 

 

BEREKENING

 

IEC 60909 en Storing sequentieel

Bij asymmetrische kortsluitberekeningen en storingsanalyses is de inverse impedantie gelijk aan de normale impedantie (Z1 = Z2 ).

De schakeling, Re, Xe, Z0 en R0 zijn niet van belang voor de berekening van een symmetrische sluiting (FFF) of een tweefasige sluiting zonder aardcontact (FF).

 

IEC 60909

Een kortsluitberekening volgens IEC 60909 kan worden bepaald met nominale trapstand of met de overzetverhouding die volgt uit de ingestelde trapstand.

Voor meer informatie, zie: http://www.phasetophase.nl/pdf/trapinstelling.pdf

De spanningsregeling is niet van invloed op de IEC 60909-berekening. Transformatoren met spanningsregeling worden voor op dezelfde wijze gemodelleerd als transformatoren zonder spanningsregeling.

 

Storing sequentieel

Transformatoren met spanningsregeling worden voor de sequentiële storingsanalyse op dezelfde wijze gemodelleerd als transformatoren zonder spanningsregeling. Wel wordt voor het bepalen van de "pre-fault" situatie (sequentie 0) een loadflow-berekening uitgevoerd. Bij deze loadflowberekening kan de trapstand worden bepaald door de spanningsregeling.